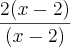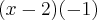por luanxd » Ter Fev 02, 2010 00:08
por luanxd » Ter Fev 02, 2010 00:08
FUVEST-SP
O conjunto verdade da equação: X+2/2 +2/x-2 = - 1/2 é:
a)(-2)
b)(-2 ;-1)
c)(2 ; -1)
d)(2)
e)(-2 ;1)
Por favor alguem pode me explicar como resolver esta equação.
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por luanxd » Ter Fev 02, 2010 17:15
por luanxd » Ter Fev 02, 2010 17:15
Ola cleyson007, obrigado pela ajuda.
Mais se voce poder me explicar melhor como voce chegou nessa parte da equação
(x-2)(x+2)+4/2(x-2) =-1(x-2)/2(x-2)
Eu agradeço.
Obrigado pela ajuda.
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Ter Fev 02, 2010 20:11
por Cleyson007 » Ter Fev 02, 2010 20:11
luanxd escreveu:Ola cleyson007, obrigado pela ajuda.
Mais se voce poder me explicar melhor como voce chegou nessa parte da equação
(x-2)(x+2)+4/2(x-2) =-1(x-2)/2(x-2)
Eu agradeço.
Obrigado pela ajuda.
Boa noite Luanxd!
Luan, eu tirei o mmc entre 2 e x - 2 (o mmc ficou 2 (x-2) )
Quanto a resolução, basta
dividir o mmc pelo
denominador da fração e o resultado que encontrar,
multiplicar pelo
numerador.
Veja melhor:

Simplificando o número 2 que aparece no numerador e no denominador, sobra

.
Lembra que o rusultado que encontrar deverá ser multiplicado pelo numerador da fração?
Por isso que ficou:

Depois do sinal de adição (+), acontece o mesmo:
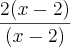
Simplicando o (x - 2) que aparece no numerador e no denominador, sobra 2.
Multiplicando pelo numerador (2 x 2 =
4)
O mesmo acontece depois da igualdade, veja:

Simplificando o 2 que aparece no numerador e no denominador, sobra (x - 2).
O resultado que encontrei deverá ser multiplicado pelo numerador (-1), daí:
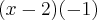
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por luanxd » Qua Fev 03, 2010 12:21
por luanxd » Qua Fev 03, 2010 12:21
Obrigado cleyson007 , por me explicar.
Mais se fosse 2/ x^2+2 + 2/x-2 =-1
Seria possível tirar o mmc ?
Obrigado pela atenção.
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7712 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13203 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13011 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6089 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8698 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


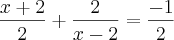

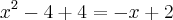
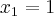





 .
.