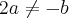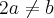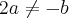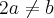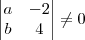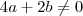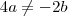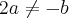por Danilo Dias Vilela » Qua Set 09, 2009 23:55
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
Gostaria que me ajudassem na seguinte questão: 1) O sistema ax-2y=1, bx+4y=5 tem solução determinada, somente se:
a)

b)
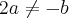
c)
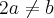
d)a= -2b (menos dois b)
e)a=b
Tenho tentado dar valores para a e para b, mas não tô conseguindo. Se alguém puder me ajudar. Molina você fez por determinantes não tem um outro jeito de fazer não? Um modo mais fácil.
Editado pela última vez por
Danilo Dias Vilela em Qui Set 10, 2009 14:41, em um total de 1 vez.
-
Danilo Dias Vilela
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Set 09, 2009 01:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Molina » Qui Set 10, 2009 14:15
por Molina » Qui Set 10, 2009 14:15
Danilo Dias Vilela escreveu:Gostaria que me ajudassem na seguinte questão: 1) O sistema ax-2y=1, bx+4y=5 tem solução determinada, somente se:
a)

b)
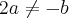
c)
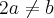
d)a= -2b (menos dois b)
e)a=b
Tenho tentado dar valores para a e para b, mas não tô conseguindo. Se alguém puder me ajudar
Boa tarde, Danilo.
Para o sistema ser determinado tem que satisfazer a inequação abaixo:
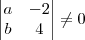
Assim:
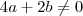
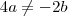
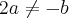
Qualquer dúvida em alguma passagem é só perguntar.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2662 Exibições
- Última mensagem por admin

Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1273 Exibições
- Última mensagem por Molina

Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1433 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 00:25
- 2 Respostas
- 2261 Exibições
- Última mensagem por RICI

Sex Ago 24, 2012 11:58
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 14:53
- 1 Respostas
- 1459 Exibições
- Última mensagem por Elcioschin

Qui Set 10, 2009 15:20
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.