Caros amigos,
Há uma questão que consigo resolver baseado nas respostas, mas a resolução sem vê-las não é possível com meu pequeno conhecimento.
Dada a equação polinomial x^3 - 7x^2 +14x -8 = 0, sabendo que uma de suas raízes é 4. É correto afirmar que o conjunto solução desta equação é:
a) {-1,1, 4}
b) {1, 2, 4}
c) {-1, -2, 4}
d) {4, i,-i} , onde i^2 = -1
e) {1, 4, 4}
Sei que tem que haver 4 na resposta, óbvio.
Mas testei -1 (não dá), testei 1 (ok) e testei 2 (ok); ou seja, a resposta correta é B => (1,2,4)
Mas fica impossível, para mim, responder sem ter as respostar para testá-las...
Obrigado pela ajuda de todos!!!



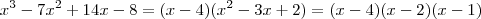
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)