 por Florisbela » Dom Mai 23, 2010 19:28
por Florisbela » Dom Mai 23, 2010 19:28
Boa noite. Como faço para resolver esse problema?
Seja "a" uma raiz da equação

, em que C é um número real positivo. Se o discriminante dessa equação é menor que zero, então encontre |a|.
-
Florisbela
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mai 23, 2010 19:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão Ambiental
- Andamento: cursando
 por DanielFerreira » Qua Jun 09, 2010 19:44
por DanielFerreira » Qua Jun 09, 2010 19:44
delta = 4 - 4c²
delta < 0
4 - 4c² < 0
- 4c² < - 4
c² > 1
c > 1


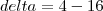

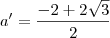
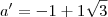
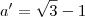
ou

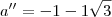
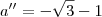
(...)

ou
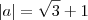
acho que é isso...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Qua Jun 09, 2010 20:35
por MarceloFantini » Qua Jun 09, 2010 20:35
Esta equação está muito estranha. Se ela tem discriminante é menor que zero, ela NÃO TEM raízes reais. Danjr, também não se esqueça que se o discriminante é menor que zero, suas respostas teria uma unidade imaginária ali, o que não acontece (porque não podemos afirmar que estamos trabalhando com os complexos).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Seg Jun 14, 2010 22:07
por DanielFerreira » Seg Jun 14, 2010 22:07
Tens razão.
não sei como transformei - 12 em + 12.

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10715 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9727 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3314 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4608 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6530 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , em que C é um número real positivo. Se o discriminante dessa equação é menor que zero, então encontre |a|.
, em que C é um número real positivo. Se o discriminante dessa equação é menor que zero, então encontre |a|.
 , em que C é um número real positivo. Se o discriminante dessa equação é menor que zero, então encontre |a|.
, em que C é um número real positivo. Se o discriminante dessa equação é menor que zero, então encontre |a|.


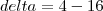

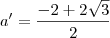
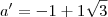
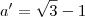

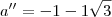
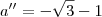

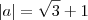






 .
.



