 por dayamtdf » Qua Mai 12, 2010 16:49
por dayamtdf » Qua Mai 12, 2010 16:49
Opa Galera Blz?
Eu Tentei fazer esse problema, já pesquisei na internet, e nos livros sobre algo relacionado, mas não obtive sucesso =/
vim aqui pedir mais uma ajuda para vocês. A questão é a seguinte:
VIII) Resolva a equação abaixo. Apresente o valor de x com, no mínimo 5 casas decimais e depois substitua o valor encontrado na equação para verificar se o valor encontrado está correto
a equação é essa:

Gostaria que vocês me ajudassem, e eu também gostaria de ajudar ao fórum, como não tenho um conhecimento muito bom em matemática, poderia ajudar financeiramente, fazendo uma doação para o fórum. Sei como é os serviços de hospedagem e etc... Não Achei nenhuma área falando sobre doações aqui no fórum...
-
dayamtdf
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 08, 2010 18:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias da Computação
- Andamento: cursando
 por dayamtdf » Qua Mai 12, 2010 20:25
por dayamtdf » Qua Mai 12, 2010 20:25
Nossa Cara, Perfeito!
Parabéns pelo seu conhecimento, Fico muito grato!
Vlw Mesmo, ainda tenho mais exercicios aqui pra fazer, vou tentar, e qualquer coisa volto aqui para pedir ajuda

Abraços.
-
dayamtdf
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 08, 2010 18:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias da Computação
- Andamento: cursando
 por Douglasm » Qua Mai 12, 2010 20:29
por Douglasm » Qua Mai 12, 2010 20:29
Estamos aqui pra isso! Bons estudos.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Kallynne » Dom Mai 16, 2010 15:45
por Kallynne » Dom Mai 16, 2010 15:45
1.A diferença dois numeros é 76.O quociente da divisão do maior pelor menor é 3, e o resto é12.Determine-os.
2.Perguntando-se a uma pessoa que idade ela tinha, ela respondeu: se do triplo de minha idade subtrairmos o queíntuplo da idade que eu tinha há 12 anos, teremos minha idadeatual. Qual a idade da pessoa?
3.Antonio fez um acordo com seu treinador . Bateria de 30 penaltis. Receberia R$ 5,00 por acerto e pagaria R$ 1,00 por erro. Ao final da brincadeira, ele recebeu R$ 120,00. Quantos penaltis ele acertou?
4. Lucas foi passar as férias na praia de Canoa Quebrada, no Ceará. Verificou que, que se gastass R$ 80,00 por dia, poderia permanecer de férias um dia a mais do que se gastasse R$ 90,00.Quanto Lucas possuia?
-
Kallynne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 16, 2010 15:32
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Matemática
- Andamento: cursando
 por Douglasm » Dom Mai 16, 2010 16:00
por Douglasm » Dom Mai 16, 2010 16:00
Olá kallynne. Quando quiser ajuda em uma questão, abra um novo tópico.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Kallynne » Dom Mai 16, 2010 16:13
por Kallynne » Dom Mai 16, 2010 16:13
que novo tópico?
-
Kallynne
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 16, 2010 15:32
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Matemática
- Andamento: cursando
 por Douglasm » Dom Mai 16, 2010 16:32
por Douglasm » Dom Mai 16, 2010 16:32
Quando quiser postar uma nova questão, abra um novo tópico. Vá em "Dúvidas Matemáticas", escolha o tema que é pertinente a sua dúvida e lá você encontrará um botão (na parte superior esquerda) dizendo "novo tópico".
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marcr7mp12 » Ter Jun 22, 2010 17:23
por marcr7mp12 » Ter Jun 22, 2010 17:23
poow ai será que vc ten como me ajudar com essa equaçao aqui
x+8=6x
x-2
ai eu fiz
(x-2).(x+8)= (x-2).6x
x-2 x-2
x2 + 8x -2x - 16 = 6x2- 12x
x2+8x-2x-16-6x2+12x=0
-5x2+18x-16=0
x(5x+18)-16
agora naun sei resolver por favor pode me ajudar !
-
marcr7mp12
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jun 22, 2010 17:08
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: inglês
- Andamento: formado
 por MarceloFantini » Qua Jun 23, 2010 02:45
por MarceloFantini » Qua Jun 23, 2010 02:45
Marc, por favor abra um novo tópico para sua dúvida.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Murta » Sáb Jun 25, 2011 21:10
por Murta » Sáb Jun 25, 2011 21:10
Kallynne escreveu:Antonio fez um acordo com seu treinador . Bateria de 30 penaltis. Receberia R$ 5,00 por acerto e pagaria R$ 1,00 por erro. Ao final da brincadeira, ele recebeu R$ 120,00. Quantos penaltis ele acertou?
-
Murta
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jun 25, 2011 21:04
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13029 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- Ajuda com equação
por Nosbor » Qui Jul 08, 2010 20:36
- 4 Respostas
- 3291 Exibições
- Última mensagem por Nosbor

Sex Jul 09, 2010 01:44
Álgebra Elementar
-
- [Equação] Ajuda
por matheusassis » Dom Set 04, 2011 14:16
- 6 Respostas
- 2564 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 18:51
Sistemas de Equações
-
- Ajuda com equação
por koh » Ter Out 04, 2011 14:31
- 0 Respostas
- 921 Exibições
- Última mensagem por koh

Ter Out 04, 2011 14:31
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em equação.
por Alynne » Seg Jan 30, 2012 12:23
- 1 Respostas
- 1218 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 30, 2012 14:27
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





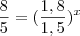
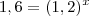
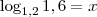

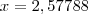 (com a aproximação de 5 casas decimais, como pede o enunciado)
(com a aproximação de 5 casas decimais, como pede o enunciado)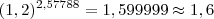




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.