 por RenataMagner » Qua Abr 07, 2010 17:31
por RenataMagner » Qua Abr 07, 2010 17:31
Oi eu estou fazendo cursinho pretendo fazer engenharia. Estou com problemas no seguinte exercício:
![\alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}} \alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}](/latexrender/pictures/6cd0bc825fcc36deae7a033c9815aeb0.png)
Conclua usando

que

é um número racional
Eu não sei por onde começar me faltam ferramentas por favor se puderem me ajudem
-
RenataMagner
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Abr 07, 2010 17:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho Pré Vestibular
- Andamento: cursando
 por RenataMagner » Qua Abr 07, 2010 22:17
por RenataMagner » Qua Abr 07, 2010 22:17
RenataMagner escreveu:Oi eu estou fazendo cursinho pretendo fazer engenharia. Estou com problemas no seguinte exercício:
![\alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}} \alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}](/latexrender/pictures/6cd0bc825fcc36deae7a033c9815aeb0.png)
Conclua usando

que

é um número racional
Eu não sei por onde começar me faltam ferramentas por favor se puderem me ajudem EU ja tentei fatorar encontrar produtos notáveis mas não saí do lugar
-
RenataMagner
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Abr 07, 2010 17:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho Pré Vestibular
- Andamento: cursando
 por MarceloFantini » Qui Abr 08, 2010 08:11
por MarceloFantini » Qui Abr 08, 2010 08:11
Tente elevar ao cubo para sumir com as raízes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por RenataMagner » Qui Abr 08, 2010 20:03
por RenataMagner » Qui Abr 08, 2010 20:03
Fantini, essa foi a primeira coisa que eu fiz porém desenvolvendo

³ eu não consigo chegar em uma expressão que me prove racionalidade. cheguei nisso daqui :
![4 + 3*(\sqrt[3]{-2-\sqrt[2]{5}} + \sqrt[3]{-2+\sqrt[2]{5}}) 4 + 3*(\sqrt[3]{-2-\sqrt[2]{5}} + \sqrt[3]{-2+\sqrt[2]{5}})](/latexrender/pictures/33acfef361741d94614cac5f3b3cef11.png)
-
RenataMagner
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Abr 07, 2010 17:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho Pré Vestibular
- Andamento: cursando
 por RenataMagner » Qui Abr 08, 2010 20:52
por RenataMagner » Qui Abr 08, 2010 20:52
Consegui eu descobri que

é racional pois
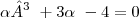
-
RenataMagner
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Abr 07, 2010 17:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho Pré Vestibular
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício Vestibular Demonstração
por RenataMagner » Qua Abr 07, 2010 17:38
- 1 Respostas
- 1550 Exibições
- Última mensagem por Neperiano

Seg Jun 28, 2010 23:16
Desafios Médios
-
- Exercício de vestibular.
por anabrizola » Qui Set 13, 2012 15:07
- 1 Respostas
- 4593 Exibições
- Última mensagem por Cleyson007

Qui Set 13, 2012 15:48
Progressões
-
- Exercício de vestibular
por Caio gomes » Seg Jul 01, 2013 17:37
- 1 Respostas
- 2900 Exibições
- Última mensagem por young_jedi

Seg Jul 01, 2013 19:39
Progressões
-
- ajuda para um exercicio de vestibular
por urb » Ter Dez 06, 2011 20:55
- 0 Respostas
- 1751 Exibições
- Última mensagem por urb

Ter Dez 06, 2011 20:55
Geometria Plana
-
- (Vestibular-80) Área
por flavio2010 » Qui Jul 15, 2010 12:54
- 2 Respostas
- 1998 Exibições
- Última mensagem por Tom

Sex Jul 16, 2010 01:38
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}} \alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}](/latexrender/pictures/6cd0bc825fcc36deae7a033c9815aeb0.png)
 que
que  é um número racional
é um número racional
![\alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}} \alpha=\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}](/latexrender/pictures/6cd0bc825fcc36deae7a033c9815aeb0.png)
 que
que  é um número racional
é um número racional
que
é um número racional



 ³ eu não consigo chegar em uma expressão que me prove racionalidade. cheguei nisso daqui :
³ eu não consigo chegar em uma expressão que me prove racionalidade. cheguei nisso daqui : ![4 + 3*(\sqrt[3]{-2-\sqrt[2]{5}} + \sqrt[3]{-2+\sqrt[2]{5}}) 4 + 3*(\sqrt[3]{-2-\sqrt[2]{5}} + \sqrt[3]{-2+\sqrt[2]{5}})](/latexrender/pictures/33acfef361741d94614cac5f3b3cef11.png)

 é racional pois
é racional pois 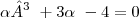


 .
.
 :
: