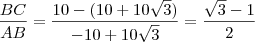por CaAtr » Sex Abr 02, 2010 16:39
por CaAtr » Sex Abr 02, 2010 16:39
No segmento AC, toma -se um ponto B de forma que


.
Entao o valor de

.
a)1/2
b)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
-1/2
c)
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png)
-1/2
d)
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png)
-1/3
Se alguem puder ajudar, nem sei por onde começa!!!
-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sex Abr 02, 2010 19:30
por Molina » Sex Abr 02, 2010 19:30
Boa tarde.
Poderia confirmar as alternativas? O 2 está dividindo apenas o número após o sinal de negativo ou está dividindo tudo (incluindo a raiz)?
Cheguei na resposta
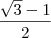
Então precisava que você confirmasse se a letra b) é essa resposta mesmo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CaAtr » Sáb Abr 03, 2010 21:10
por CaAtr » Sáb Abr 03, 2010 21:10
Sim sim é a alternativa b!!
Se puder me demonstrar como fez, agradeço!!
Desculpe - me, nao ter esclarecido melhor as alternativas!!
Abraços
-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Abr 03, 2010 22:56
por Molina » Sáb Abr 03, 2010 22:56
CaAtr escreveu:Sim sim é a alternativa b!!
Se puder me demonstrar como fez, agradeço!!
Desculpe - me, nao ter esclarecido melhor as alternativas!!
Abraços
Boa noite.
Minha tentativa pra resolver essa questão foi dar um valor pro segmento AC (e pelo jeito deu certo). Considerei valendo 10. E o segmento AB valendo x:

______________
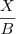
_____________________________

Sendo assim:




E resolvendo isso vai dar numa equação do 2° grau:

Resolvendo, uma raiz será positiva e a outra negativa (descartaremos esta).

(este é o valor de x, que é o ponto B).
Queremos descobrir quanto vale

:
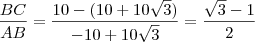
Fiz aqui sem muitos detalhes. Se em alguma parte o resultado não bater, informe que eu posto aqui, ok?
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CaAtr » Dom Abr 04, 2010 14:25
por CaAtr » Dom Abr 04, 2010 14:25
Ah sim sim!!!
Mas ali na equaçao do 2 grau:
é x² + 20x - 200 = 0 ne?? Creio que esqueceu do x!!
Bom obrigada pela ajuda, jamais imaginaria resolver assim! Do resto bateu tudo sim!!
Obrigada e bom domigo de Pascoa!!
-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Abr 04, 2010 14:27
por Molina » Dom Abr 04, 2010 14:27
CaAtr escreveu:Ah sim sim!!!
Mas ali na equaçao do 2 grau:
é x² + 20x - 200 = 0 ne?? Creio que esqueceu do x!!
Bom obrigada pela ajuda, jamais imaginaria resolver assim! Do resto bateu tudo sim!!
Obrigada e bom domigo de Pascoa!!
Opa, é isso mesmo, tem o x ali. Valeu pelo toque, vou editar e deixar certinho.
Feliz Páscoa pra vc tb! =)
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest-SP
por luanxd » Dom Fev 07, 2010 20:16
- 4 Respostas
- 5419 Exibições
- Última mensagem por luanxd

Ter Fev 09, 2010 11:06
Sistemas de Equações
-
- LOG FUVEST
por PHANIE » Ter Abr 12, 2011 13:22
- 1 Respostas
- 14741 Exibições
- Última mensagem por Molina

Ter Abr 12, 2011 15:13
Logaritmos
-
- FUVEST 1
 por PHANIE » Ter Abr 26, 2011 15:53
por PHANIE » Ter Abr 26, 2011 15:53
- 3 Respostas
- 14138 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:17
Geometria Plana
-
- fuvest 2
por PHANIE » Ter Abr 26, 2011 15:57
- 3 Respostas
- 5027 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:33
Geometria Plana
-
- fuvest
por karen » Qua Nov 28, 2012 14:48
- 1 Respostas
- 1297 Exibições
- Última mensagem por young_jedi

Qua Nov 28, 2012 16:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 .
. .
.![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) -1/2
-1/2![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) -1/2
-1/2![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) -1/3
-1/3
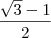



 ______________
______________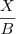 _____________________________
_____________________________





 (este é o valor de x, que é o ponto B).
(este é o valor de x, que é o ponto B). :
: