primeiramente peço minhas desculpas aos colegas,leitores e estudantes desse site,pois editei erroneamente a primeira equaçao do sistema...vamos ao sistema correto e sua soluçao:
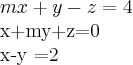
quando resolvemos um sistema de equaçao,procuramos os pontos em comuns das equaçoes,que podem ser pontos,retas,planos,superficies,hiperplanos etc...
o nosso sistema é de equaçoes lineares de primeiro grau,ou seja,todas as incognitas(x,y,z)tem potencia igual a 1.
nosso sistema é de 3 equaçoes,3 incognitas...vamos usar a "regra de cramer",pois o sistema é de poucas incognitas.
como tambem existe o "rouche-capelli",que é mais eficiente quando se trata de "discutir o sistema"."discutir o sistema" é saber as condiçoes de solubilidade,ou nao...e em caso de soluvel,achar os valores dessas incognitas...
tomamos o determinante da matriz incompleta
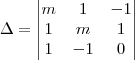
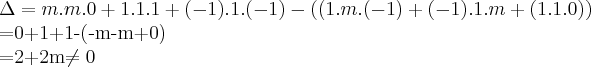
para se ter soluçao...
e
para se ter ou nao soluçao...m=-1,nao tera pois,o sistema
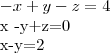
subst. (3) em (2)
z=-2...subst. z,x,y na (1)
por adauto martins » Qua Set 18, 2019 13:24 
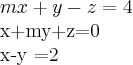
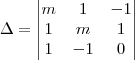
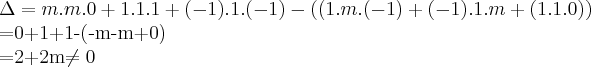
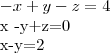
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)