 por Amanda185 » Ter Jun 04, 2013 23:34
por Amanda185 » Ter Jun 04, 2013 23:34
(UECE) Para r ? 2, se x = p e y = q é a solução do sistema linear
![f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right] f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right]](/latexrender/pictures/82ed058560f8b858762fbfe02a3fc3d3.png)
, então o valor de p² + q² é:
Fiz o determinante das matrizes e cheguei até: r² - 4, mas como o r não pode ser 2 não sei o que fazer...
-
Amanda185
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 22, 2013 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por DanielFerreira » Qua Jun 05, 2013 01:27
por DanielFerreira » Qua Jun 05, 2013 01:27
Amanda,
a questão parece-me interessante, no entanto, antes de respondê-la gostaria de saber se ela está completa. Têm as alternativas??
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Amanda185 » Qua Jun 05, 2013 14:37
por Amanda185 » Qua Jun 05, 2013 14:37
Sim. As alternativas são:
a) 0
b) 1
c) 2
d) 4
-
Amanda185
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 22, 2013 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por DanielFerreira » Qua Jun 05, 2013 22:59
por DanielFerreira » Qua Jun 05, 2013 22:59
Como disse anteriormente, temos aqui uma questão bem interessante! Concluí que a alternativa correta é a
letra c.

Encontramos o 'valor' de

substituindo

por
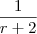
em uma das equações acima.

Observe que

, então,

; por conseguinte
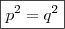
!
Daí, nada mais podemos concluir!!
No entanto, fiz umas buscas na "net" e notei que o seu enunciado está diferente, se comparado ao original.
Segue,
Para

, se

e

é a solução do sistema linear
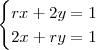
, então o valor de

é:
a) 1
b) 2
c) 4
d) 0
Concluímos que

, então:

Portanto,
alternativa d.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Amanda185 » Qui Jun 06, 2013 00:09
por Amanda185 » Qui Jun 06, 2013 00:09
Ah siiimm, peguei o enunciado desse jeito, copiada no quadro. Muito Obrigada pela ajuda!

-
Amanda185
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 22, 2013 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas Lineares
por Cleyson007 » Sáb Mai 03, 2008 01:50
- 3 Respostas
- 7040 Exibições
- Última mensagem por admin

Dom Mai 04, 2008 13:51
Sistemas de Equações
-
- Sistemas Lineares
por gustavowelp » Sáb Jun 26, 2010 17:05
- 3 Respostas
- 7801 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 09:09
Sistemas de Equações
-
- Sistemas lineares
por Catriane Moreira » Seg Set 06, 2010 18:32
- 1 Respostas
- 2492 Exibições
- Última mensagem por Molina

Seg Set 06, 2010 19:13
Sistemas de Equações
-
- sistemas lineares
por angeloka » Sáb Nov 27, 2010 17:59
- 1 Respostas
- 2635 Exibições
- Última mensagem por Neperiano

Sáb Nov 27, 2010 19:02
Sistemas de Equações
-
- sistemas lineares
 por angeloka » Sáb Nov 27, 2010 22:10
por angeloka » Sáb Nov 27, 2010 22:10
- 0 Respostas
- 1817 Exibições
- Última mensagem por angeloka

Sáb Nov 27, 2010 22:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right] f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right]](/latexrender/pictures/82ed058560f8b858762fbfe02a3fc3d3.png) , então o valor de p² + q² é:
, então o valor de p² + q² é:
![f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right] f(x)=\left[rx + 2y = 1 \right]
\left[2x + ry = 1 \right]](/latexrender/pictures/82ed058560f8b858762fbfe02a3fc3d3.png) , então o valor de p² + q² é:
, então o valor de p² + q² é:



 substituindo
substituindo  por
por 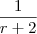 em uma das equações acima.
em uma das equações acima.
 , então,
, então,  ; por conseguinte
; por conseguinte 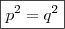 !
!, se
e
é a solução do sistema linear
, então o valor de
é:
 , então:
, então:



