Uma caixa contém porcas e parafusos. Cada parafuso pesa o dobro de uma porca. O peso bruto da caixa é de 2500g e a embalagem corresponde a 4% do peso bruto. Qual a quantidade de parafusos da caixa sabendo -se que o total de peças e 100 e que cada porca pesa 20g.
parafuso = 2x20= 40
porca = 20
total peças = 100
peso bruto = 2500g
peso liquido= 2500 x 4%= 100g
Peso bruto - peso liquido = 2400
Não consigo montar uma equação pra resolver esse problema. Por favor me ajudem.
Desde ja agradeço




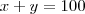
 e
e  .
. parafusos
parafusos porcas
porcas
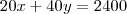
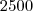




 .
.



