Se você calcular o determinante dos coeficientes verá que o resultado é zero. Por que? A resposta é: tome a primeira equação e some à segunda. Você terá exatamente a terceira equação, a menos do termo independente. Ou seja, o sistema não pode ser possível e determinado, resta descobrir se é impossível ou indeterminado. Se

, que corresponde à soma das equações, então ele será indeterminado pois teremos mais equações do que incógnitas. Se
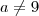
, então ele será impossível.
Geometricamente, tudo isto significa que temos três planos, onde um é combinação dos outros dois. O termo independente diz o quanto ele está "deslocado" em relação aos outros. Quando o termo independente for igual a

teremos que ele não está deslocado e sim coincide com a combinação dos outros dois; se
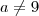
então ele está deslocado e não há interseção com os outros dois planos, portanto o sistema é impossível.
No segundo sistema, como o determinado é não-nulo para qualquer valor de

(escolhi uma letra grega), isto significa que ele será possível e determinado, cuja única solução é zero independentemente de

.
Por último, quando você tem mais incógnitas do que equações isto significa que você tem poucas figuras geométricas se interseccionando, no caso de sistemas lineares você terá planos. Nestes casos você deve verificar se eles são paralelos (ou seja, se os coeficientes de um são múltiplos dos coeficientes do outro, por exemplo
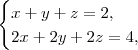
onde temos que a segunda é múltipla da segunda), e se forem descobrir se o termo independente for múltiplo também; caso não seja, os planos são paralelos e não coincidentes e portanto não há solução. Se não forem múltiplos, então com certeza há interseção e será uma reta.




 , que corresponde à soma das equações, então ele será indeterminado pois teremos mais equações do que incógnitas. Se
, que corresponde à soma das equações, então ele será indeterminado pois teremos mais equações do que incógnitas. Se 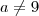 , então ele será impossível.
, então ele será impossível.  (escolhi uma letra grega), isto significa que ele será possível e determinado, cuja única solução é zero independentemente de
(escolhi uma letra grega), isto significa que ele será possível e determinado, cuja única solução é zero independentemente de 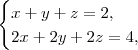


 , avisa que eu resolvo.
, avisa que eu resolvo.

