 por thyago_1 » Dom Jun 17, 2012 20:31
por thyago_1 » Dom Jun 17, 2012 20:31
-
thyago_1
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jun 17, 2012 20:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Programação de Jogos Digitais
- Andamento: cursando
 por e8group » Dom Jun 17, 2012 22:24
por e8group » Dom Jun 17, 2012 22:24
Boa noite thyago_1 ,Como você tentou resolver ? por favor ,mostre seu desenvolvimento para assim melhor podermos ajuda-lo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thyago_1 » Dom Jun 17, 2012 22:38
por thyago_1 » Dom Jun 17, 2012 22:38
Olá Santhiago, recebi este exercicío e estou tentando resolver o mesmo no momento. Postei ele aqui, para que pudesse ter ajuda da galera na resolução do mesmo. De qualquer forma terei a resolução em mãos daqui a 2 dias e caso ninguém consiga resolver por aqui, eu posto a resolução.
Abraços!
-
thyago_1
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jun 17, 2012 20:19
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Programação de Jogos Digitais
- Andamento: cursando
 por e8group » Qua Jun 20, 2012 16:48
por e8group » Qua Jun 20, 2012 16:48
i)

ii)
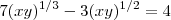
Primeiramente para o sistema ter solução temos

e

> 0 .
Assim ,
![7(xy)^{1/3} - 3(xy)^{1/2} =7[(xy)^{1/6} ]^2 -3[(xy)^{1/6}]^3 = 4 7(xy)^{1/3} - 3(xy)^{1/2} =7[(xy)^{1/6} ]^2 -3[(xy)^{1/6}]^3 = 4](/latexrender/pictures/200503cf970e3af1e5f7a4af40f1b613.png)
.
Fazendo

.Temos :

Da eq. i) temos :

,Lembrando que

e

> 0 ,ou seja :
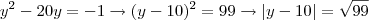
, pela definição de modulo ,temos :

e

.
Solução :

e

.
Se não cometi algum erro estar certo ....
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4493 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5533 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3344 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3591 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  :
: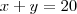
![7 \sqrt[3] {xy} - 3\sqrt{xy} = 4 7 \sqrt[3] {xy} - 3\sqrt{xy} = 4](/latexrender/pictures/c84d278c7fbf6b495bd6ed747f6bca34.png)

 e
e  :
: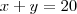
![7 \sqrt[3] {xy} - 3\sqrt{xy} = 4 7 \sqrt[3] {xy} - 3\sqrt{xy} = 4](/latexrender/pictures/c84d278c7fbf6b495bd6ed747f6bca34.png)




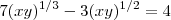
 e
e  > 0 .
> 0 .![7(xy)^{1/3} - 3(xy)^{1/2} =7[(xy)^{1/6} ]^2 -3[(xy)^{1/6}]^3 = 4 7(xy)^{1/3} - 3(xy)^{1/2} =7[(xy)^{1/6} ]^2 -3[(xy)^{1/6}]^3 = 4](/latexrender/pictures/200503cf970e3af1e5f7a4af40f1b613.png) .
. .Temos :
.Temos : 
 ,Lembrando que
,Lembrando que  e
e  > 0 ,ou seja :
> 0 ,ou seja :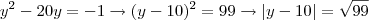 , pela definição de modulo ,temos :
, pela definição de modulo ,temos : e
e  .
. e
e  .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)