 por TAE » Sex Jun 01, 2012 00:00
por TAE » Sex Jun 01, 2012 00:00
Boa noite, só uma pequena dúvida o porquê de não estar dando b=-2.
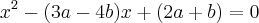
. Raízes da equação 3 e 4. Determine a e b.

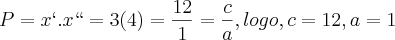
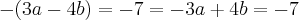

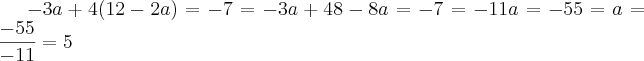

Resposta:
a=5
b=2
Valeu.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por Russman » Sex Jun 01, 2012 01:34
por Russman » Sex Jun 01, 2012 01:34
Você deve montar um sistema!

Agora, resolva-o!
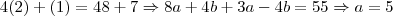
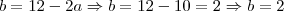
Veja que aplicando estes valores na equação obtemos
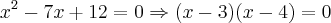
cuja solução é
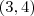
, como se qeria!
Você fez certo! Porqe teria de calcular

?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por TAE » Sex Jun 01, 2012 16:57
por TAE » Sex Jun 01, 2012 16:57
Foi mal pela, confusão é o que o livro está dando b=-2, então o gabarito deve estar errado, muito obrigado pela ajuda.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar a Equação da Hiperbole...
por Mystic_Fan » Ter Jun 07, 2011 23:49
- 1 Respostas
- 1532 Exibições
- Última mensagem por DanielFerreira

Qui Jun 16, 2011 16:45
Geometria Analítica
-
- [circunferência] determinar a equação
por Fabio Wanderley » Qui Abr 26, 2012 11:23
- 1 Respostas
- 3217 Exibições
- Última mensagem por LuizAquino

Qui Abr 26, 2012 16:16
Geometria Analítica
-
- [Determinar equação da Parábola]
 por aliceleite » Ter Set 04, 2012 20:20
por aliceleite » Ter Set 04, 2012 20:20
- 1 Respostas
- 1531 Exibições
- Última mensagem por Russman

Qua Set 05, 2012 01:31
Funções
-
- [ Determinar a equação do plano]
por lucasdemirand » Dom Set 01, 2013 00:12
- 0 Respostas
- 664 Exibições
- Última mensagem por lucasdemirand

Dom Set 01, 2013 00:12
Álgebra Linear
-
- Determinar equação da elipse
por fernandabalvin » Qua Mar 08, 2017 15:36
- 0 Respostas
- 2053 Exibições
- Última mensagem por fernandabalvin

Qua Mar 08, 2017 15:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
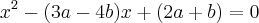 . Raízes da equação 3 e 4. Determine a e b.
. Raízes da equação 3 e 4. Determine a e b.
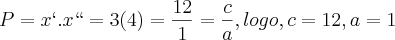
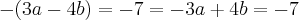

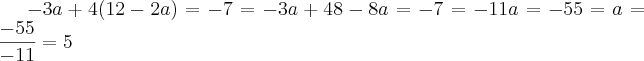


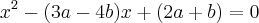 . Raízes da equação 3 e 4. Determine a e b.
. Raízes da equação 3 e 4. Determine a e b.
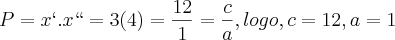
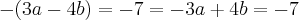

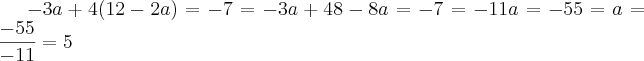



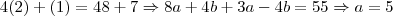
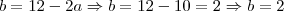
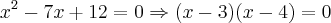
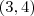 , como se qeria!
, como se qeria! ?
?
