 por tajas » Dom Mai 06, 2012 11:21
por tajas » Dom Mai 06, 2012 11:21
Precisava de saber a resposta para estas 2 equaçoes por favor, ja tentei de tudo e nao consigo, me ajudem

.
(5^x) -3 * 5^(-2x)=0
e
(2^x) -6 * (2^-x) -1 =0
-
tajas
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 06, 2012 11:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Mai 06, 2012 15:54
por MarceloFantini » Dom Mai 06, 2012 15:54
É fundamental lembrar o fato que
 sempre
sempre que

. Isto significa que

e
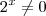
para todo
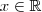
.
Para resolver o primeiro problema, ponha
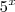
em evidência e atente para o fato que quando

então

ou

. Relacione a informação anterior com esta.
Para o segundo multiplique a equação inteira por
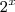
e depois faça a mudança de variável

. Você perceberá um polinômio do segundo grau. Resolva e volte para a variável original, não esquecendo do conceito fundamental da exponencial.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- EXPOENTES
por RODRIGO DE FARIA » Qui Jan 17, 2013 00:34
- 3 Respostas
- 2905 Exibições
- Última mensagem por RODRIGO DE FARIA

Sex Jan 25, 2013 12:29
Álgebra Elementar
-
- Log e expoentes fracionários
por sergioereis1 » Dom Abr 20, 2014 06:51
- 0 Respostas
- 2346 Exibições
- Última mensagem por sergioereis1

Dom Abr 20, 2014 06:51
Logaritmos
-
- Simplicação trabalhando expoentes.
por Rafael Sposito » Dom Fev 17, 2013 17:51
- 1 Respostas
- 1451 Exibições
- Última mensagem por young_jedi

Dom Fev 17, 2013 23:47
Álgebra Elementar
-
- Potencias com expoentes diferentes - Subtrair?
por Soprano » Dom Fev 14, 2016 10:25
- 7 Respostas
- 7587 Exibições
- Última mensagem por Soprano

Dom Fev 14, 2016 17:05
Números Complexos
-
- [DÚVIDA] Potências de expoentes racionais e raízes.
por invader_zim » Ter Fev 12, 2013 11:31
- 3 Respostas
- 2344 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 12:24
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.
 .
.
 sempre que
sempre que  . Isto significa que
. Isto significa que  e
e 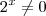 para todo
para todo 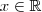 .
.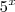 em evidência e atente para o fato que quando
em evidência e atente para o fato que quando  então
então  ou
ou  . Relacione a informação anterior com esta.
. Relacione a informação anterior com esta.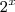 e depois faça a mudança de variável
e depois faça a mudança de variável  . Você perceberá um polinômio do segundo grau. Resolva e volte para a variável original, não esquecendo do conceito fundamental da exponencial.
. Você perceberá um polinômio do segundo grau. Resolva e volte para a variável original, não esquecendo do conceito fundamental da exponencial.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.