Problemas de equação do primeiro grau III

[Andrewo]

Aí galera, tenho meus últimos probleminhas aqui de equação do 1º grau, que precisava da ajuda de vocês, não pra resolver, mas pra me explicar como colocar isso matematicamente.




1-Na hora de fazer seu testamento, uma pessoa tomou a seguinte decisão: dividiria sua fortuna entre a sua filha, que está grávida, e a prole resultante dessa gravidez, dando a cada criança que fosse nascer o dobro daquilo que caberia a mãe se fosse do sexo masculino, e o trilho daquilo que caberia a mãe se fosse do sexo feminino.Nasceram trigêmeos, sendo dois meninos e uma menina.Como veio a ser repartida a herança legada?
Resposta: para a mãe, para cada menino e para cada menina.



2-Em uma sala de aula, dos alunos (meninos e meninas) eram meninas.Dobrando-se o número de meninos e acrescentando-se 6 meninas, o número de meninos ficou igual ao número de meninas.Então o produto do nº de meninos pelo nº de meninas será:
Resposta:216



3-A soma das idades de 4 irmãos é 76 anos.Se a soma das idades dos 3 mais novos excede em 32 anos a idade do mais velho, então a idade do mais velho é:
Resposta:22 anos



4-Para manter funcionando um chuveiro elétrico durante um banho de 15 minutos e um forno microondas durante 5 minutos, as quantidades de água que precisam passar pelas turbinas de certa usina hidrelétrica são, respectivamente, 4000 litros e 200 litros.Suponha que, para esses eletrodomésticos, a redução de consumo será proporcional à redução da quantidade de água que passa pelas turbinas.Com base nisso, se o banho for reduzido para nove minutos e o tempo de utilização do microondas for reduzido de 20% a quantidade total de água utilizada na usina para movimentar as turbinas, durante o banho mais o uso do microondas, será, após as reduções, de :
Resposta:2560

[MarceloFantini]

Andrewo, não poste listas de exercício, esta não é a função do fórum. Poste cada enunciado separadamente e com suas tentativas.

[Andrewo]

Pô brother, eu conheço bem as regras, minha intenção não é que resolvam pra mim não, eu quero é aprender a fazer.Como eu posso postar tentativa se eu não sei nem mesmo por onde começar?

[MarceloFantini]

Então poste apenas uma questão, não várias. Te ajudarei com a primeira, as outras você colocará separadamente em novos tópicos e terá novas ajudas, ok?

Vamos analisar o problema. Se a mãe tivesse um garoto, ela ganharia e o garoto ganharia pois o enunciado diz:

[...] dando a cada criança que fosse nascer o dobro daquilo que caberia a mãe se fosse do sexo masculino, [...]

Se a mãe tiver uma garota, ela ganharia e a garota ganharia , pois o enunciado diz:

[...] e o triplo daquilo que caberia a mãe se fosse do sexo feminino. [...]

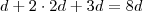Já interpretamos como funciona com cada criança. Agora, é dito que a mãe tem trigêmeos, dois meninos e uma menina. Sendo assim, a mãe ganhará , cada menino ganha e a menina ganhará . O total será . A proporção então será para a mãe, para cada menino e para a menina.