 por -Rafael- » Sex Fev 24, 2012 14:00
por -Rafael- » Sex Fev 24, 2012 14:00
Boa tarde, meu problema e o seguinte:
Foi autorizado um aumento de 40% no preço de um artigo, mas a industria resolveu aumentar apenas 80% da taxa autorizada. Qual a porcentagem do aumento que teve o artigo ?
Bom, eu basicamente so consegui compreender uma coisa que os 80% equivale aos 40%. Mas como eu consigo montar a equação para descobrir a %.
eu posso dizer que : x(artigo) + 40 = x ? e do resultado disso falar 80% - 40% = X ? so que ai não da certo .. se poderem me ajudar ficarei agradecido.
-
-Rafael-
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 24, 2012 13:50
- Formação Escolar: SUPLETIVO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por timoteo » Sex Fev 24, 2012 17:17
por timoteo » Sex Fev 24, 2012 17:17
primeiro devemos transformar a porcentagem em decimal e depois utlizar a forma decimal das pocentagens.
sendo P o produto entao P x 0,4 = a e P + a = A ( A = aumento relativo).
fazendo uma formula na outra temos: P + P x 0,4 = A <---> P ( 1 + 0,4) = A.
agora vamos subtrair com os 0,8, para isso precisamos saber sobre que esse percentual recai, que no caso é o valor a, entao:
a ( 1 - 0,8) = D, (D= desconto). fazendo A - D = R, (R= valor real aumentado).
agora para encontrarmos o percentual de aumento colocaremos R na primeira equaçao e substituiremos 0,4 por y, assim ficamos:
P ( 1 + y ) = R, y nesse caso é o percentual real do aumento.
P.S. dê uma olhada em forma decimal das percentagens.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por DanielFerreira » Sáb Fev 25, 2012 02:09
por DanielFerreira » Sáb Fev 25, 2012 02:09
-Rafael- escreveu:Boa tarde, meu problema e o seguinte:
Foi autorizado um aumento de 40% no preço de um artigo, mas a industria resolveu aumentar apenas 80% da taxa autorizada. Qual a porcentagem do aumento que teve o artigo ?
Bom, eu basicamente so consegui compreender uma coisa que os 80% equivale aos 40%. Mas como eu consigo montar a equação para descobrir a %.
eu posso dizer que : x(artigo) + 40 = x ? e do resultado disso falar 80% - 40% = X ? so que ai não da certo .. se poderem me ajudar ficarei agradecido.
Preço atual: k
Após aumento autorizado: k + 40% . k
Decisão da indústria: k + 80% . 40% . k

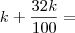

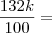
Montemos uma regra de três simples:
R$ k -------------------------------------------- 100%
R$

--------------------------------------- x

%
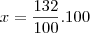
%
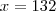
%
Daí,
132% - 100% =
32%"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por -Rafael- » Sáb Fev 25, 2012 12:21
por -Rafael- » Sáb Fev 25, 2012 12:21
Muito Obrigado me ajudarao muito .. isso e matematica basica que eu reprovei semestre passado '-' ..
-
-Rafael-
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 24, 2012 13:50
- Formação Escolar: SUPLETIVO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por timoteo » Sáb Fev 25, 2012 13:10
por timoteo » Sáb Fev 25, 2012 13:10
quando eu desejo somar um valor eu computo assim:
p ( 1 + x/100) = valor com aumento. ex: p=100, x= 30%. 100( 1 + 30/100)= 130, esse valor ja esta somado.
agora para subtrair é preciso que vc utilize a o complementar do valor que vc deseja aumentar. ex: desejo subtrair 30% de 100 entao eu uso o complementar e fica assim: 0,7 x 100 = 70 que é o valor ja com desconto. entao sabendo disso temos:
P (1 + 0,4 x 0,2 )= P mais o aumento real. fazendo 0,4 x 0,2 = 0,08 que é o valor percentual do aumento.
o equivoco de Dan é que ele fez 80% sobre o valor que ja tinha aumentado, o problema é que com esse novo valor vc tem que subtrai-lo do valor conseguido da primeira multiplicaçao por 40%.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por DanielFerreira » Sáb Fev 25, 2012 13:30
por DanielFerreira » Sáb Fev 25, 2012 13:30
Timoteo,
interpretei assim o problema:
Supondo que o valor do artigo seja R$ 100,00; autorizaram 40% de aumento, então, o novo valor será (100 + 40% . 100 = 100 + 40 = R$ 140,00).
Entendo que R$ 40,00 seja a taxa autorizada, por isso, calculei:
80% . R$ 40,00 =
R$ 32,00
Ou seja, decidiram aumentar apenas R$ 32,00 em vez de R$ 40,00.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por timoteo » Sáb Fev 25, 2012 15:14
por timoteo » Sáb Fev 25, 2012 15:14
Dan, eu compreende seu ponto de vista. porem da maneira que vc faz teremos que subtrrair 32 de 40 e por fim encontrar 8 e este somado com 100 nos dará 108, valor real do aumento. faça na calcuradora o que lhe disse no outro post. pra soma utilize 100 ( 1 + x/100)= R e para subtraçao faça: R ( 1 - x/100)= p, agora utilize p no lugar de R na primeira equaçao.
................
temos tbm que: R ( 1 - x/100) <--> R (100% - x%/100) = p
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por -Rafael- » Seg Fev 27, 2012 11:22
por -Rafael- » Seg Fev 27, 2012 11:22
timoteo escreveu:Dan, eu compreende seu ponto de vista. porem da maneira que vc faz teremos que subtrrair 32 de 40 e por fim encontrar 8 e este somado com 100 nos dará 108, valor real do aumento. faça na calcuradora o que lhe disse no outro post. pra soma utilize 100 ( 1 + x/100)= R e para subtraçao faça: R ( 1 - x/100)= p, agora utilize p no lugar de R na primeira equaçao.
................
temos tbm que: R ( 1 - x/100) <--> R (100% - x%/100) = p
eu fiz desse jeito .. ficou facil de entender tbm .. brigadao msm
-
-Rafael-
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 24, 2012 13:50
- Formação Escolar: SUPLETIVO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7716 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13209 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13017 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8702 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




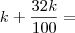

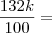
 --------------------------------------- x
--------------------------------------- x %
%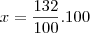 %
%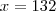 %
%


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.