 por Robinho » Sáb Jan 14, 2012 12:51
por Robinho » Sáb Jan 14, 2012 12:51
Meu trabalho tem 123 questões falta pouco agora mais ha algumas que ta meio complicado e eu nao consigo fazer!
Dá pra vocês me ajudar nessa aqui tambem!!!
O quociente

é igual á:

-
Robinho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 12:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Sáb Jan 14, 2012 13:09
por MarceloFantini » Sáb Jan 14, 2012 13:09
Qual foi a sua tentativa?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Robinho » Sáb Jan 14, 2012 13:20
por Robinho » Sáb Jan 14, 2012 13:20
Cara principalmente essa do quociente eu nem sei por onde começa nao tenho ideia de como seje as que eu sabia fazer mais ou menos eu ja fazia
sosinho!
Eu to te perguntano como faz ´pq eu nem tenho noção intende

-
Robinho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 12:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quociente por Médias
por yonara » Qua Jun 09, 2010 15:08
- 1 Respostas
- 1795 Exibições
- Última mensagem por MarceloFantini

Qua Jun 09, 2010 20:40
Estatística
-
- Inequação quociente
 por Bruno Pinheiro » Ter Dez 28, 2010 01:12
por Bruno Pinheiro » Ter Dez 28, 2010 01:12
- 3 Respostas
- 3029 Exibições
- Última mensagem por MarceloFantini

Qua Dez 29, 2010 10:45
Álgebra Elementar
-
- Derivada do Quociente
 por dekol2 » Dom Mai 06, 2012 20:39
por dekol2 » Dom Mai 06, 2012 20:39
- 4 Respostas
- 4289 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
-
- Inequação Quociente
por MERLAYNE » Qua Mai 09, 2012 11:08
- 2 Respostas
- 1652 Exibições
- Última mensagem por DanielFerreira

Qua Mai 09, 2012 22:48
Sistemas de Equações
-
- [Derivada] Quociente
por Paraujo » Dom Set 23, 2012 21:15
- 9 Respostas
- 6556 Exibições
- Última mensagem por Paraujo

Ter Set 25, 2012 12:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é igual á:
é igual á:

 é igual á:
é igual á:




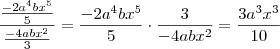


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.