 por guillcn » Qua Out 26, 2011 15:24
por guillcn » Qua Out 26, 2011 15:24
O enunciado diz:
O Conjunto soluçao da equaçao
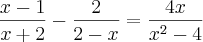
é :
entao comecei a resoluçao :
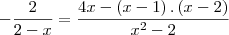
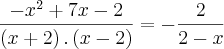
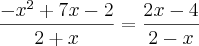
E fui continuando mas nao chegeui no resultado.O resultado e x=3,alguem poderia me ajudar com a resoluçao deste exercicio?
Obrigado pela Atençao.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Neperiano » Qua Out 26, 2011 17:43
por Neperiano » Qua Out 26, 2011 17:43
Ola
Você pode tirar da baskara emcima, e depois multiplicar como uma regra de três
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por guillcn » Seg Nov 21, 2011 17:57
por guillcn » Seg Nov 21, 2011 17:57
Se eu utilizar baskara a raiz de delta sera 41 e ai na hora de multiplicar em cruz vira uma bagunça nao consegui resolver o exercicio.voce tem mais alguma outra forma para resolver o problema?obrigado pela ajuda.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Nov 21, 2011 18:12
por MarceloFantini » Seg Nov 21, 2011 18:12
Note:
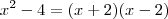
e

, logo
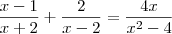
, daí
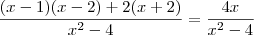
, e portanto podemos afirmar

, tente terminar. Perceba que

e

pelas condições de existência.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por guillcn » Ter Nov 22, 2011 17:18
por guillcn » Ter Nov 22, 2011 17:18
eu continuei a resolução
(x-1).(x-2)+2.(2+x)=4x
x²-3x+2+2x+4=4x
x²-5x+6=0
V={3,2}
Mas o resultado esta errado ,o resultado certo e V={3}.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Nov 22, 2011 18:55
por MarceloFantini » Ter Nov 22, 2011 18:55
Você não prestou atenção na parte que eu disse

e

pelas condições de existência, a função não está definida aí e portanto é óbvio que não está no conjunto solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3752 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- Quadrado Perfeito?
por Molina » Qui Nov 25, 2010 17:00
- 6 Respostas
- 6677 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 16:28
Desafios Difíceis
-
- Quadrado perfeito
por guillcn » Ter Abr 05, 2011 19:15
- 2 Respostas
- 2514 Exibições
- Última mensagem por guillcn

Ter Abr 05, 2011 19:54
Álgebra Elementar
-
- Ajuda com quadrado perfeito
por joaoalbertotb » Ter Ago 25, 2009 13:01
- 2 Respostas
- 2305 Exibições
- Última mensagem por joaoalbertotb

Qua Ago 26, 2009 12:20
Trigonometria
-
- Trinômio Quadrado Perfeito
por Balanar » Ter Ago 10, 2010 22:48
- 2 Respostas
- 4920 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 18:05
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
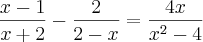 é :
é :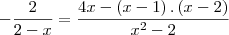
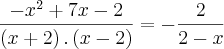
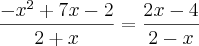

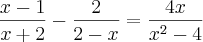 é :
é :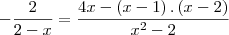
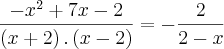
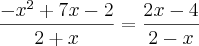



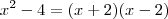 e
e  , logo
, logo 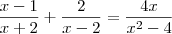 , daí
, daí 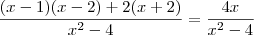 , e portanto podemos afirmar
, e portanto podemos afirmar  , tente terminar. Perceba que
, tente terminar. Perceba que  e
e  pelas condições de existência.
pelas condições de existência.


 e
e  pelas condições de existência, a função não está definida aí e portanto é óbvio que não está no conjunto solução.
pelas condições de existência, a função não está definida aí e portanto é óbvio que não está no conjunto solução.
