Boa Noite Amigos.
É a minha primeira dúvida aqui neste fórum, espero poder compartilhar experiências juntos, bom vamos ao que enteressa:
Um posto presta serviço para os seus clientes, atendendo 3 tipo de automóveis: carro de passeio, camionete e caminhões. O valor cobrado para o carro de passeio é R$17,00, camionetes R$25,00 e caminhões R$30,00. Em um final de semana foram atendidos 24 veículos e o valor arrecadado foi de R$506,00. Sabe-se que o numero de carros de passeio superou os demais em duas unidades. Resolva o sistema correspondente:
X+Y+Z=24
17X+25Y+30Z=506
x=2+y+z
Acho que montei o sistema corretamente? Tranquei nesta parte, não sei como montar o resto da equação, se alguém puder me dar uma luz,não quero a resposta mas se puderem me dar uma dica fico muito agradecido.






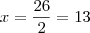
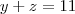
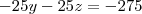


 , avisa que eu resolvo.
, avisa que eu resolvo.

