por Raphael Feitas10 » Ter Mar 29, 2011 15:16
por Raphael Feitas10 » Ter Mar 29, 2011 15:16
Calcule o valor de n para que o inteiro da forma
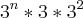
admita 8 divisores positivos. R:4
Fiz ate aqui brother mas ñ achei a resposta me ajuda aew...
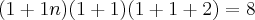
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Ter Mar 29, 2011 16:47
por FilipeCaceres » Ter Mar 29, 2011 16:47
Para saber o número de divisores de um número, primeiro devemos fatorar em números primos
Ex.:
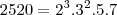
Assim temos que o número de divisores será:
Número de divisores de 2 520 = (3 + 1) · (2 + 1) · (1 + 1) · (1 + 1) = 48
Desta forma, para a questão proposta, temos:
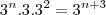
Logo,o número de divisores de
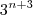
:
(n+3+ 1)=8
Portanto,
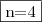
Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros primos mutlipos e divisiros 24
por Raphael Feitas10 » Sex Fev 25, 2011 01:17
- 4 Respostas
- 2034 Exibições
- Última mensagem por Renato_RJ

Sex Fev 25, 2011 14:50
Funções
-
- Numeros primos mutlipos e divisiros 28
por Raphael Feitas10 » Ter Abr 12, 2011 01:10
- 5 Respostas
- 1998 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 12, 2011 14:55
Funções
-
- Numeros primos mutlipos e divisiros 43
por Raphael Feitas10 » Sex Ago 12, 2011 01:46
- 1 Respostas
- 883 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 08:25
Sistemas de Equações
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17176 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 4103 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
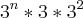 admita 8 divisores positivos. R:4
admita 8 divisores positivos. R:4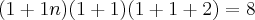

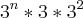 admita 8 divisores positivos. R:4
admita 8 divisores positivos. R:4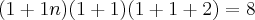

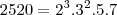
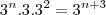
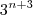 :
: