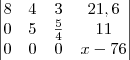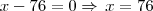por fernandocez » Ter Mar 01, 2011 12:11
por fernandocez » Ter Mar 01, 2011 12:11
Caro amigos, venho mais uma vez pedir ajuda. A questão envolvendo sistema de equações tá me dando dor de cabeça. Vamos a bendita questão.
54. Em certa papelaria todos os lápis tem o mesmo preço, todas as borrachas tem o mesmo preço e todas as canetas tem o mesmo preço. Comprando 8 lápis, 4 borrachas e 3 canetas você pagará R$ 21,60. Comprando 6 lápis, 8 borrachas e 4 canetas você pagará R$ 27,20. Uma compra de 20 lápis, 20 borrachas e 11 canetas custará:
resposta: R$ 76,00.
Eu fiz o seguinte:
8l + 4b+ 3c = 21,60
6l + 8b + 4c = 27,20
20l + 20b + 11c = x
Eu ía tentar por escalonamento de sistema, multiplicar umas das esquações e somar com outra prá cancelar uma das incógnitas. Mas percebi que tinha o "x", achei que assim não ía dar. Resolvi fazer por adição só nas 2 primeiras mas não deu certo. Só com as duas primeiras no sist. de escalonamento o "c" volta a aparecer:
8l + 4b+ 4c = 21,60
14l +- 8b = 4,8
Se eu continuasse o "c" voltaria e tinha que fazer de novo.
Tem um modo mais fácil de encontrar os valores de L, B, C? Na prova depende de tempo e é o que não tem. Aguardo uma ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Ter Mar 01, 2011 12:41
por LuizAquino » Ter Mar 01, 2011 12:41
Dica: multiplique toda a segunda equação por 2 e em seguida some com a primeira equação.
Editado pela última vez por
LuizAquino em Ter Mar 01, 2011 12:42, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Ter Mar 01, 2011 12:42
por Renato_RJ » Ter Mar 01, 2011 12:42
Bom dia Fernando, tudo em paz ??
Seguinte amigão, eu consegui resolver usando escalonamento mesmo, veja:
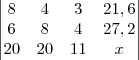
Eu fiz
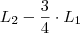
para eliminar o 6 da primeira coluna da segunda linha, veja:
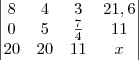
Depois eu fiz
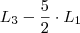
para eliminar o 20 da primeira coluna da terceira linha, veja:
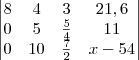
Para eliminar o 10 (da segunda coluna da terceira linha) eu simplesmente fiz
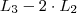
, então:
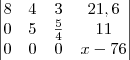
Logo, teremos:
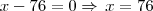
Espero ter ajudado..
[ ] 's
Renato
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por fernandocez » Ter Mar 01, 2011 13:01
por fernandocez » Ter Mar 01, 2011 13:01
LuizAquino escreveu:Dica: multiplique toda a segunda equação por 2 e em seguida some com a primeira equação.
Renato_RJ escreveu:Bom dia Fernando, tudo em paz ??
Seguinte amigão, eu consegui resolver usando escalonamento mesmo, veja:
Obrigado pessoal, vcs são muito feras, seu estivesse nesse nível passaria com folga no concurso, mas tenho que estudar muito mesmo. Um abração.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Ter Mar 01, 2011 13:06
por Renato_RJ » Ter Mar 01, 2011 13:06
Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Se você se cadastra na SBM recebe um desconto de 25% para cada compra, a maioria desses livros acaba custando R$ 18,00, acho que vale a pena (eles entregam pelos correios)...
Segue o link para a coleção da qual eu falei:
http://loja.sbm.org.br/index.php?cPath= ... 09b81659ae[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Ter Mar 01, 2011 13:41
por LuizAquino » Ter Mar 01, 2011 13:41
Olá fernandocez,
Uma curiosidade: onde você fez a sua graduação em Licenciatura em Matemática?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Ter Mar 01, 2011 20:56
por fernandocez » Ter Mar 01, 2011 20:56
Renato_RJ escreveu:Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Valeu a dica renato vou comprar sim, uma pergunta: a linguagem não é muito "pesada" desses livros? Porque eu tenho alguns da coleção Fundamentos de mat. elementar e acho muito difícil entender.
LuizAquino escreveu:Olá fernandocez,
Uma curiosidade: onde você fez a sua graduação em Licenciatura em Matemática?
O Luiz, vc sempre me ajudando nas questões. Sobre o meu curso, eu fiz na Unigranrio em Caxias - RJ, mas não culpem a instituição eu é que caí de paraquedas lá. Eu comecei a fazer informática (2 períodos), desisti e troquei pela Matemática pra arrumar emprego com mais facilidade o que não aconteceu. Eu me formei em 2009 e até agora não consegui nenhum colégio prá lecionar. Já coloquei uns 40 currículos mas nenhum vingou, nem se quer fui a uma entrevista. Agora tô apostando nesse concurso e nos próximos.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Ter Mar 01, 2011 21:48
por Renato_RJ » Ter Mar 01, 2011 21:48
fernandocez escreveu:Renato_RJ escreveu:Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Valeu a dica renato vou comprar sim, uma pergunta: a linguagem não é muito "pesada" desses livros? Porque eu tenho alguns da coleção Fundamentos de mat. elementar e acho muito difícil entender.
Grande Fernando, essa coleção é do Iezzi certo ?? Se for, é a mesma que eu tenho aqui, e te digo, os livros da SBM são mais profundos pois trazem as demonstrações necessárias para a compreensão do conteúdo, fora que seus exercícios são bem mais complicados. Mas se você tem o Iezzi, estude por ele, é um excelente livro...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema equações] questão de concurso 2011
por fernandocez » Qua Out 05, 2011 22:32
- 9 Respostas
- 6425 Exibições
- Última mensagem por fernandocez

Sáb Out 08, 2011 15:33
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4493 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- SISTEMA DE EQUAÇÃO PROVA SENAI
por hatredshadows » Sex Nov 08, 2013 08:17
- 3 Respostas
- 3298 Exibições
- Última mensagem por e8group

Sex Nov 08, 2013 20:53
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5533 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3344 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



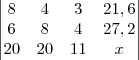
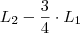 para eliminar o 6 da primeira coluna da segunda linha, veja:
para eliminar o 6 da primeira coluna da segunda linha, veja: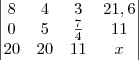
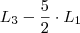 para eliminar o 20 da primeira coluna da terceira linha, veja:
para eliminar o 20 da primeira coluna da terceira linha, veja: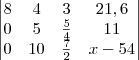
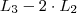 , então:
, então: