(Marcelo Fantini e demais usuários do ajuda mat.) Aproveitando o tópico para ampliar o conhecimento , a parti de uma matriz quadrada (identidade ) ou (diagonal ) eu consigo obter uma matriz genérica tal que exista a comutatividade do produto .
Exemplo : se
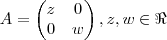
ou

.
Ou seja para ambos casos existe uma matriz

tal que

.Entretanto para duas matrizes genéricas
![A = \begin{pmatrix} x & z \\ w & y \end{pmatrix} , [A]_{ij} \in \Re A = \begin{pmatrix} x & z \\ w & y \end{pmatrix} , [A]_{ij} \in \Re](/latexrender/pictures/14afd3ff1a391d9101860b440845a0ea.png)
e
![B =\begin{pmatrix} a & b \\ c & d\end{pmatrix},[B]_{ij} \in \Re B =\begin{pmatrix} a & b \\ c & d\end{pmatrix},[B]_{ij} \in \Re](/latexrender/pictures/a2c355f9e1365542bec5e691a96dc5b9.png)
Será que eu consigo estabelecer uma condição para

através de um sistema linear de tal forma que
![[AB]_{ij} = [BA]_{ij} [AB]_{ij} = [BA]_{ij}](/latexrender/pictures/7981eb7bfdca055df30dfe7139ebabf2.png)
?
Eu fiz isso mas chegou em um ponto difícil de obter uma condição que satisfaz cada equação ,analiticamente impossível . Será que com algum software tais como wxMaxima e etc consigo encontrar algo ?
Será que isso realmente prova uma condição para comutação do produto ?
Obrigado .


 , e mais,
, e mais, 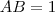 , onde 1 é a matriz identidade. Ser diagonal também é uma condição para comutarem. A questão é que muito difícil, dadas duas matrizes genéricas, descobrir se o produto comuta ou não.
, onde 1 é a matriz identidade. Ser diagonal também é uma condição para comutarem. A questão é que muito difícil, dadas duas matrizes genéricas, descobrir se o produto comuta ou não.

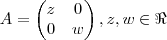 ou
ou  .
. tal que
tal que  .Entretanto para duas matrizes genéricas
.Entretanto para duas matrizes genéricas ![A = \begin{pmatrix} x & z \\ w & y \end{pmatrix} , [A]_{ij} \in \Re A = \begin{pmatrix} x & z \\ w & y \end{pmatrix} , [A]_{ij} \in \Re](/latexrender/pictures/14afd3ff1a391d9101860b440845a0ea.png) e
e ![B =\begin{pmatrix} a & b \\ c & d\end{pmatrix},[B]_{ij} \in \Re B =\begin{pmatrix} a & b \\ c & d\end{pmatrix},[B]_{ij} \in \Re](/latexrender/pictures/a2c355f9e1365542bec5e691a96dc5b9.png)
![[AB]_{ij} = [BA]_{ij} [AB]_{ij} = [BA]_{ij}](/latexrender/pictures/7981eb7bfdca055df30dfe7139ebabf2.png) ?
? 
 .
.



