 por Pri Ferreira » Seg Mai 21, 2012 22:55
por Pri Ferreira » Seg Mai 21, 2012 22:55
Se A=
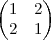
e B=
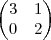
, o produto entre os determinantes das matrizes X = (

x A)t e Y = (A + B)
será igual a:
A) 0/6 B) 3/6 C) 6/6 D) 9/6 E) 12/6
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por MarceloFantini » Ter Mai 22, 2012 02:11
por MarceloFantini » Ter Mai 22, 2012 02:11
Pri Ferreira, quais foram suas tentativas? Você já resolveu algum problema semelhante?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Pri Ferreira » Ter Mai 22, 2012 21:44
por Pri Ferreira » Ter Mai 22, 2012 21:44
Obrigada pela ajuda.
Foi o q eu fiz, mas não encontrei a resposta entre as opções.
Eu encontro 30,625 e a resposta é 29,9.
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 11271 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
-
- Questão de concurso
por bia rosendo » Qua Fev 23, 2011 11:00
- 4 Respostas
- 5787 Exibições
- Última mensagem por Elcioschin

Qui Fev 24, 2011 11:08
Funções
-
- Questão de concurso
 por bia rosendo » Seg Fev 28, 2011 22:54
por bia rosendo » Seg Fev 28, 2011 22:54
- 2 Respostas
- 7734 Exibições
- Última mensagem por LuizAquino

Ter Mar 01, 2011 14:12
Problemas do Cotidiano
-
- QUESTAO CONCURSO..
por PathyNorato » Qui Jul 07, 2011 15:59
- 1 Respostas
- 3501 Exibições
- Última mensagem por FilipeCaceres

Qui Jul 07, 2011 21:05
Matemática Financeira
-
- questão de concurso
por luciana-lopfer » Qui Nov 24, 2011 14:34
- 5 Respostas
- 6349 Exibições
- Última mensagem por Tiago_Cariolano

Seg Jan 16, 2012 01:23
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
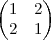 e B=
e B=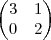 , o produto entre os determinantes das matrizes X = (
, o produto entre os determinantes das matrizes X = ( x A)t e Y = (A + B)
x A)t e Y = (A + B)
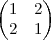 e B=
e B=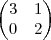 , o produto entre os determinantes das matrizes X = (
, o produto entre os determinantes das matrizes X = ( x A)t e Y = (A + B)
x A)t e Y = (A + B)



