 por Claudin » Qui Fev 09, 2012 18:57
por Claudin » Qui Fev 09, 2012 18:57
Considerando a matriz
0 3 5
2 -5 4
1 2 1
Para encontrar a inversa, pelo modo que eu quero deve-se fazer o seguinte
Fazer a matriz aumentada com a identidade
e ir escalonando. Correto? Se for invertível a matriz inversa após o escalonamento se formará na direita e na esquerda seria a Identidade.
Porém pelo método de Gauss Jordan, como iniciarei o escalonamento sendo que a¹¹ = 0 ?
Não tem como passar ele para 1, para que comece o escalonamento.
E ai oq eu faço?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Fev 09, 2012 20:12
por MarceloFantini » Qui Fev 09, 2012 20:12
Se você somar a terceira linha a menos a primeira você terá

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Sex Fev 10, 2012 10:36
por Claudin » Sex Fev 10, 2012 10:36
Cheguei em um resultado muito estranho, está errado, vou refazer, se alguém postar o início do desenvolvimento já ajuda.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Fev 10, 2012 11:29
por LuizAquino » Sex Fev 10, 2012 11:29
Claudin escreveu:Considerando a matriz
0 3 5
2 -5 4
1 2 1
Para encontrar a inversa, pelo modo que eu quero deve-se fazer o seguinte
Fazer a matriz aumentada com a identidade
e ir escalonando. Correto? Se for invertível a matriz inversa após o escalonamento se formará na direita e na esquerda seria a Identidade.
Porém pelo método de Gauss Jordan, como iniciarei o escalonamento sendo que a¹¹ = 0 ?
Não tem como passar ele para 1, para que comece o escalonamento.
E ai oq eu faço?
Claudin escreveu:Cheguei em um resultado muito estranho, está errado, vou refazer, se alguém postar o início do desenvolvimento já ajuda.
Comece fazendo a operação
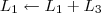
:
![\left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right]](/latexrender/pictures/10ad4caffa4ade108485e7c9f4a66be8.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sex Fev 10, 2012 19:33
por Claudin » Sex Fev 10, 2012 19:33
A inversa seria?
5 4 35
-2 -3 -14
1 2 6
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Fev 10, 2012 21:25
por MarceloFantini » Sex Fev 10, 2012 21:25
Tente multiplicar pela matriz original e veja se o resultado é a identidade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Fev 11, 2012 02:41
por LuizAquino » Sáb Fev 11, 2012 02:41
Claudin escreveu:A inversa seria?
5 4 35
-2 -3 -14
1 2 6
Como você já deve saber (e bem lembrou o colega
MarceloFantini), ao multiplicar essa matriz pela original o resultado deve ser a identidade, caso essa matriz seja de fato a inversa da original.
Após fazer essa multiplicação, você perceberá que não é o caso.
A inversa correta é:
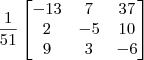 Observação
ObservaçãoÉ interessante que você comece a usar um
sistema computacional algébrico. Um sistema como esse será muito útil em seus estudos. Particularmente, eu recomendo o
SAGE.
Vale também ressaltar que você pode calcular a inversa de uma matriz usando o sistema online
WolframAlpha. Basta executar no campo de entrada do sistema o comando:
- Código: Selecionar todos
{{0, 3, 5}, {2, -5, 4}, {1, 2, 1}}^(-1)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Seg Fev 13, 2012 11:30
por Claudin » Seg Fev 13, 2012 11:30
Já conheço o programa sim.
Mas na hora da prova eu não terei esse programa, por isso gostaria de ver o desenvolvimento
para ajudar a entender.
Foi o que eu sempre tentei mostrar isso aqui no Fórum.
Continuo sem compreender como resolver
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Seg Fev 13, 2012 13:55
por Claudin » Seg Fev 13, 2012 13:55
Não intendi esse termo que multiplica a sua inversa no caso acima?
Achei alguns erros e fiz novamente,
O que eu encontrei foi o seguinte:
![\left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left \left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left](/latexrender/pictures/a8f7ef10416b77057eb890f47cd3c40b.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Fev 13, 2012 14:43
por LuizAquino » Seg Fev 13, 2012 14:43
Claudin escreveu:Já conheço o programa sim.
Ok.
Claudin escreveu:Mas na hora da prova eu não terei esse programa (...)
Isso é verdade. Mas enquanto você estiver estudando, pode utilizar o programa para conferir a sua resposta.
Em uma de suas mensagens, você perguntou:
Claudin escreveu:A inversa seria?
5 4 35
-2 -3 -14
1 2 6
Note que você poderia utilizar o programa para conferir isso. Ou ainda, você mesmo poderia conferir manualmente a sua resposta fazendo a seguinte multiplicação:
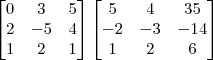
Se essa multiplicação resultar na matriz identidade, então a inversa foi calculada corretamente. Caso contrário, algum erro foi cometido.
Vale lembrar que na hora da prova você também não terá a sua disposição esse fórum para pedir ajuda. É recomendado que você aprenda a conferir a sua resposta manualmente.
Claudin escreveu:(...) por isso gostaria de ver o desenvolvimento para ajudar a entender.
Foi o que eu sempre tentei mostrar isso aqui no Fórum.
Continuo sem compreender como resolver
Na sua primeira mensagem, você perguntou:
Claudin escreveu:Porém pelo método de Gauss Jordan, como iniciarei o escalonamento sendo que a¹¹ = 0 ?
Não tem como passar ele para 1, para que comece o escalonamento.
E ai oq eu faço?
Em seguida, você comentou:
Claudin escreveu:Cheguei em um resultado muito estranho, está errado, vou refazer, se alguém postar o início do desenvolvimento já ajuda.
Depois disso, eu mostrei para você o início assim como você pediu:
Comece fazendo a operação
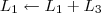
:
![\left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right]](/latexrender/pictures/0300efe2f869d7ff98c3bd10e5f5c0e9.png)
Entretanto, você ainda continua com dúvidas. Eu vou então continuar os passos.
2º Passo)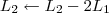

![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/d56718e58c14e6be4a675798d0b2c218.png) 3º Passo)
3º Passo)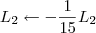
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/bf92d321716c471edd90a6d9d4a9323d.png) 4º Passo)
4º Passo)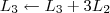
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right]](/latexrender/pictures/8bbd6a7495d616b3577aeb425fd217a5.png) 5º Passo)
5º Passo)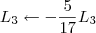
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/a18e87a70e18a740ac1a1e48d3e9a375.png) 6º Passo)
6º Passo)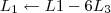
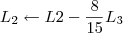
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/61fdfca5f5d28b7cf66be0a778fedbbb.png) 7º Passo)
7º Passo)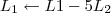
![\left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/95113ef6e8f4c96b29789121f4cc76a3.png)
Podemos então reescrever a resposta final como:
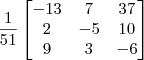
Para conferir o resultado, basta efetuar a operação:
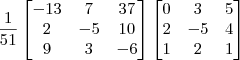
Note que o resultado dessa operação será a matriz identidade.
ObservaçãoSe você deixasse para transformar os pivôs em 1 apenas no final do processo (como expliquei em
seu outro tópico), você iria economizar tempo realizando menos operações com frações.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Seg Fev 13, 2012 15:33
por Claudin » Seg Fev 13, 2012 15:33
Muito obrigado pela explicação Luiz Aquino
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7151 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3568 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6722 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4692 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4802 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.

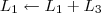 :
:![\left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right]](/latexrender/pictures/10ad4caffa4ade108485e7c9f4a66be8.png)
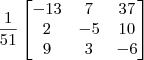
![\left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left \left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left](/latexrender/pictures/a8f7ef10416b77057eb890f47cd3c40b.png)
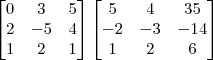
![\left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right]](/latexrender/pictures/0300efe2f869d7ff98c3bd10e5f5c0e9.png)
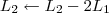

![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/d56718e58c14e6be4a675798d0b2c218.png)
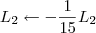
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/bf92d321716c471edd90a6d9d4a9323d.png)
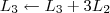
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right]](/latexrender/pictures/8bbd6a7495d616b3577aeb425fd217a5.png)
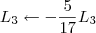
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/a18e87a70e18a740ac1a1e48d3e9a375.png)
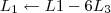
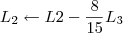
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/61fdfca5f5d28b7cf66be0a778fedbbb.png)
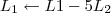
![\left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/95113ef6e8f4c96b29789121f4cc76a3.png)
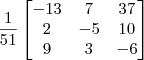
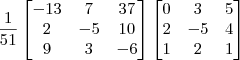
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: