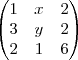


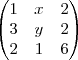

angela sofia Pereira escreveu:considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace, explicitando os pontos x e y para os quais a matriz é invertivel. Já tentei resolver de várias formas mas não chego a nenhuma conclusão, pedia um pequeno auxilio para solucionar esta questão.

LuizAquino escreveu:angela sofia Pereira escreveu:considerando a seguinte matriz pede-se para calcular o determinante da matriz como função de x e y por expansão de Laplace, explicitando os pontos x e y para os quais a matriz é invertivel. Já tentei resolver de várias formas mas não chego a nenhuma conclusão, pedia um pequeno auxilio para solucionar esta questão.
Por favor, envie a sua resolução para que possamos identificar o erro.

angela sofia Pereira escreveu:(...) a minha duvida é se o que é pedido é apenas o determinante desta matriz que já calculei e dava 2y-14x+4 ou se em primeiro lugar tenho de achar as variáveis x e y de n sei como fazer (...)





Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante