fabiosousa escreveu:Olá Cleyson, boa noite!
Como a matriz original é de ordem 2, obtemos o determinante pelo produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária.
Sugiro refazer e enviar suas contas.
Olá Fabio Sousa.
Realmente eu resolvi dessa maneira (o produto dos elementos da diagonal principal menos o produto dos elementos da diagonal secundária)!!!
Resolvendo ficou o seguinte:
![\frac{\sqrt[]{2}}{2} - \sqrt[]{8} \frac{\sqrt[]{2}}{2} - \sqrt[]{8}](/latexrender/pictures/c3fe9d8c351b31ceca6e368c1bf8fb31.png)
.
Não domino muito bem esse editor de fórmulas, por isso vai ser complicado explicar como que eu fiz até chegar aonde vou dizer, mas sei que até onde cheguei está correto.
Cheguei a essa conclusão:
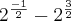
.
Para resolver, o que eu encontrei (essa conclusão que descrevi acima), fiz algo que na verdade não sei se pode ser feito (considerei a base (2) e o sinal de menos lembrei que em exponenciais indicava divisão).
Ficou o seguinte:

(dois elevado a meio menos três meios).
Resolvendo encontrei o valor de

.
Está correto?
Ajude-me por favor!!!
Peço desculpas pelos transtornos em ter que entender o que estou tentando dizer, mas, espero que tenha dado para entender!!!
![\begin{vmatrix}
\frac{1}{2} & \sqrt[]{8} \\
1 & \sqrt[]{2}
\end{vmatrix} \begin{vmatrix}
\frac{1}{2} & \sqrt[]{8} \\
1 & \sqrt[]{2}
\end{vmatrix}](/latexrender/pictures/df426a9649aeb54edc13d82d327b9e26.png) .
.![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png) e
e ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) para base 2.
para base 2.![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png) ficou o seguinte:
ficou o seguinte: ![2 \sqrt[2]{2} 2 \sqrt[2]{2}](/latexrender/pictures/b93adb28140c708054c32b796f175e32.png) .
. ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ficou o seguinte:
ficou o seguinte:  .
. .
.




![\frac{\sqrt[]{2}}{2} - \sqrt[]{8} \frac{\sqrt[]{2}}{2} - \sqrt[]{8}](/latexrender/pictures/c3fe9d8c351b31ceca6e368c1bf8fb31.png) .
. .
. (dois elevado a meio menos três meios).
(dois elevado a meio menos três meios). em evidência para simplificar a expressão, tente assim.
em evidência para simplificar a expressão, tente assim.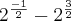 está correto não é?
está correto não é?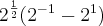
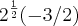
![{2}^{\frac{1}{2}} = \sqrt[]{2} {2}^{\frac{1}{2}} = \sqrt[]{2}](/latexrender/pictures/feb59a6d3c7d8c7f9c76791508d62d64.png) obtive como resposta:
obtive como resposta: ![-3\sqrt[2]{2}/2 -3\sqrt[2]{2}/2](/latexrender/pictures/74b21effb2ead33599e08cf08bcd2a78.png) .
.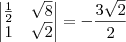
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.