Estou com uma questão de determinantes para resolver, e gostaria de saber se está correto o procedimento por mim adotado para a resolução da mesma. Desde já agradeço a atenção de todos.
A questão é essa----> Dada
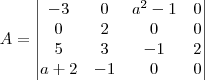 .
.(a) Determine todos os valores de
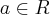 (conjunto dos números reais), para que detA = 0.
(conjunto dos números reais), para que detA = 0.(b) Escolha um destes valores de
 e, para este valor escolhido, dê exemplos de matrizes colunas
e, para este valor escolhido, dê exemplos de matrizes colunas 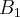 e
e  (4x1) tais que
(4x1) tais que tenha solução e
tenha solução e  não tenha.
não tenha.A letra (a) resolvi da seguinte maneira ---> Optei por calcular o determinante de
 (por ser a linha que contém o maior número de zeros).
(por ser a linha que contém o maior número de zeros).Resolvendo o determinante pelo cofator do elemento
 , encontrei a seguinte equação:
, encontrei a seguinte equação: 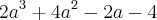
Resolvendo a equação, encontrei
 ,
,  e
e  .
.Quanto a (b) não consegui entender o enunciado, gostaria que me desse alguma dica a fim de que compreenda o mesmo!!!
Forte abraço!!!
Até mais.



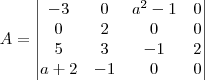 .
. é uma matriz. Entretanto, você escreveu
é uma matriz. Entretanto, você escreveu 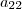 é um elemento da matriz. Você escreveu algo diferente do pretendido.
é um elemento da matriz. Você escreveu algo diferente do pretendido.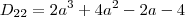
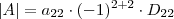
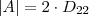

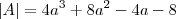
 , o fator
, o fator  não influenciará nas raízes desta cúbica:
não influenciará nas raízes desta cúbica: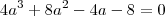
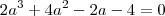

 é uma matriz.
é uma matriz.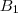 e
e 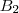 são matrizes 4x1,
são matrizes 4x1, 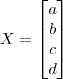



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.