-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477742 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528690 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492244 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 696777 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2105589 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por manuoliveira » Seg Set 06, 2010 01:34
por manuoliveira » Seg Set 06, 2010 01:34
(FUVEST) A equação matricial

admite mais de uma solução se, e somente se,

é igual a:
Resposta: +-

-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por manuoliveira » Seg Set 06, 2010 11:40
por manuoliveira » Seg Set 06, 2010 11:40
Obrigada!!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por rafael_ferramenteiro » Dom Mai 18, 2014 15:05
por rafael_ferramenteiro » Dom Mai 18, 2014 15:05
-
rafael_ferramenteiro
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 18, 2014 14:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação matricial
por SAAMS » Dom Nov 28, 2010 17:18
- 0 Respostas
- 3443 Exibições
- Última mensagem por SAAMS

Dom Nov 28, 2010 17:18
Matrizes e Determinantes
-
- Equação matricial ????
por thyerry01 » Qui Set 26, 2013 02:06
- 2 Respostas
- 17198 Exibições
- Última mensagem por thyerry01

Sex Set 27, 2013 01:48
Matrizes e Determinantes
-
- A solução da equação matricial
por diogenesos » Sex Fev 10, 2012 01:52
- 1 Respostas
- 12366 Exibições
- Última mensagem por LuizAquino

Sex Fev 10, 2012 11:03
Matrizes e Determinantes
-
- Calcule o valor de m na equação matricial A*X=B
por andersontricordiano » Seg Jan 16, 2012 19:46
- 3 Respostas
- 3450 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 18, 2012 23:52
Matrizes e Determinantes
-
- Determinar a matriz X na Equação matricial AX=B
por hugo guedes » Qui Mar 12, 2015 10:37
- 1 Respostas
- 23455 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 25, 2015 16:58
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 admite mais de uma solução se, e somente se,
admite mais de uma solução se, e somente se,  é igual a:
é igual a:

 admite mais de uma solução se, e somente se,
admite mais de uma solução se, e somente se,  é igual a:
é igual a:










![\lambda=\pm\sqrt[]{11} \lambda=\pm\sqrt[]{11}](/latexrender/pictures/2a3636cc9cb43128f726edf287c62339.png) o sistema homogêneo deve ser da seguinte forma:
o sistema homogêneo deve ser da seguinte forma:
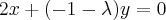
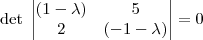

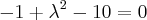


![\lambda=\pm\sqrt[]{11} \lambda=\pm\sqrt[]{11}](/latexrender/pictures/2a3636cc9cb43128f726edf287c62339.png)

