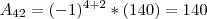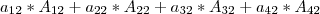Sendo cada elemento da matriz dado por

onde "i" representa a linha desse elemento e "j" sua coluna, podemos calcular o det como segue:
1º: Escolha uma linha ou coluna da matriz. Dê preferencia por uma que tenha mais 0's, pois irá facilitar os calculos.
2º: Calcular os cofatores dos elementos da linha/coluna selecionada.
O cofator de um elemento é dado por:


é o
determinante da matriz inicial após eliminarmos tanto a coluna quanto a linha das quais o elemento

pertence.
3º: Tendo os cofatores de cada um dos elementos da linha/coluna selecionada poderemos calcular o det. O
determinante é dado somando cada cofator multiplicado por seu respectivo elemento.
Parece complicado, mas pelo exemplo fica bem facil:
a) Vamos escolher a coluna 2.
Vamos ter que calcular os cofatores dos elementos:
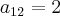
,

,
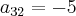
,

->

:

->

:

->
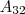
:

->
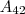
:
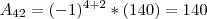
Agora podemos calcular o determiannte:
Det =
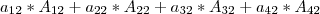
Det = 2*(-151) + 6*187 + (-5)*(-160) + (-3)*140
Det = 1200
As outras seguem da mesma forma.
Espero ter ajudado, qualquer duvida deixe msg.



 onde "i" representa a linha desse elemento e "j" sua coluna, podemos calcular o det como segue:
onde "i" representa a linha desse elemento e "j" sua coluna, podemos calcular o det como segue:
 é o determinante da matriz inicial após eliminarmos tanto a coluna quanto a linha das quais o elemento
é o determinante da matriz inicial após eliminarmos tanto a coluna quanto a linha das quais o elemento  pertence.
pertence.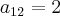 ,
,  ,
, 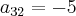 ,
, 
 :
: 
 :
: 
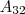 :
: 
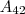 :
: