 por Jamilly » Qua Mar 17, 2010 22:40
por Jamilly » Qua Mar 17, 2010 22:40
Tenho dúvida em uma questão de determinante!
Como se acha o determinante em uma matriz 4x4?
O exercício é esse:
a) Descreva a matriz A=[aij]4x4, cujo termo geral é definido por aij=i-j: Resposta: Eu resolvi e deu:
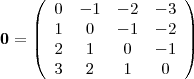
Acho que está certo.
b) Calcule a det(A):Resposta: Não consegui fazer, pois só sei fazer det de matriz de ordem até 3.
c) Com base no item anterior, responda (*justificando) se o sistema homogêneo AX=0, qm que X e 0, possui soluções não triviais.
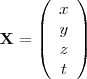
e

Resposta: Essa tbm eu não entendi!!
Me ajudem por favor!!

-
Jamilly
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Mar 11, 2010 10:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por Elcioschin » Qui Mar 18, 2010 13:30
por Elcioschin » Qui Mar 18, 2010 13:30
Sugiro que vc estude:
Determinantes ----> Menor Complementar e Cofator ----> Determinante de uma matriz de ordem n > 3 ---->
Teorema de Laplace ----> Propriedades de Determinantes ----> Regra de Chió
Como vc pode ver, o assunto é vasto e fica complicado ensinar tudo aquí. Portanto, mãos à obra!!!!
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
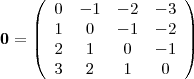
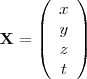





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.