 por Souo » Qua Abr 22, 2015 12:05
por Souo » Qua Abr 22, 2015 12:05
O determinante da matriz
![\left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right] \left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right]](/latexrender/pictures/c78ccb072764a734a62ce9da1b9fa0ef.png)
é nulo para m igual a:
A) -6 ou 0
B) -2 ou 1
C) -2 ou 2
D) 0 ou 6
E) 0 ou 2
No gabarito a resposta certa esta como letra A, mas cheguei em outra resposta alguém poderia me explicar?
-
Souo
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Abr 14, 2015 20:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qui Abr 23, 2015 15:41
por DanielFerreira » Qui Abr 23, 2015 15:41

Souo, encontre as raízes da equação e terá a resposta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Souo » Qui Abr 23, 2015 22:57
por Souo » Qui Abr 23, 2015 22:57
Só uma duvida, é
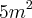
pq esta multiplicando né, se fosse somado seria 6m?
-
Souo
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Abr 14, 2015 20:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Souo » Qui Abr 23, 2015 23:05
por Souo » Qui Abr 23, 2015 23:05
Pra encontrar as raízes preciso fazer por Bhaskara, ou tem outro jeito?
-
Souo
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Abr 14, 2015 20:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sex Abr 24, 2015 21:11
por DanielFerreira » Sex Abr 24, 2015 21:11
Souo escreveu:Só uma duvida, é
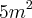
pq esta multiplicando né, se fosse somado seria 6m?
Isso!
Souo escreveu:Pra encontrar as raízes preciso fazer por Bhaskara, ou tem outro jeito?
Existem outras formas, entretanto, se não estiveres familiarizado com Bhaskara, sugiro que encontre as raízes aplicando tal método.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinantes
por Cleyson007 » Dom Jul 20, 2008 11:55
- 1 Respostas
- 5187 Exibições
- Última mensagem por admin

Dom Jul 20, 2008 18:58
Matrizes e Determinantes
-
- determinantes..
por GABRIELA » Ter Set 15, 2009 20:12
- 2 Respostas
- 3859 Exibições
- Última mensagem por GABRIELA

Qui Set 17, 2009 18:13
Matrizes e Determinantes
-
- determinantes
por carolina camargo » Sáb Jul 10, 2010 18:03
- 1 Respostas
- 3112 Exibições
- Última mensagem por Molina

Dom Jul 11, 2010 15:21
Álgebra Elementar
-
- determinantes
por carolina camargo » Sáb Jul 10, 2010 18:08
- 1 Respostas
- 2915 Exibições
- Última mensagem por Tom

Sáb Jul 10, 2010 23:16
Álgebra Elementar
-
- Determinantes
por aline2010 » Seg Jul 19, 2010 14:13
- 1 Respostas
- 3292 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 19:26
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right] \left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right]](/latexrender/pictures/c78ccb072764a734a62ce9da1b9fa0ef.png) é nulo para m igual a:
é nulo para m igual a:
![\left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right] \left[\begin{array}{cccc} _{m+5} & _{m+3} \\ _{3m+10} & _{5m+6}\\\end{array}\right]](/latexrender/pictures/c78ccb072764a734a62ce9da1b9fa0ef.png) é nulo para m igual a:
é nulo para m igual a:


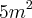 pq esta multiplicando né, se fosse somado seria 6m?
pq esta multiplicando né, se fosse somado seria 6m?

pq esta multiplicando né, se fosse somado seria 6m?

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.