 por Drudi_Fer » Dom Jan 19, 2014 16:33
por Drudi_Fer » Dom Jan 19, 2014 16:33
Tentei resolver este exercício mas o gabarito não esta de acordo com minha resposta gostaria de uma resolução para detectar possíveis erros meus ou do gabarito
1.Sejam as matrizes A = (aij)3x3, tal que aij = i – 3j, B = (bij)3x3,
tal que bij = 2j + i2, e C = (cij)3x3, tal que cij = ix j. Então a
soma dos elementos da diagonal principal da matriz Q,
onde Q = A + B – C, é
-
Drudi_Fer
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jan 19, 2014 16:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Educação Física
- Andamento: formado
 por e8group » Seg Fev 03, 2014 20:30
por e8group » Seg Fev 03, 2014 20:30
Uma matriz

que se exprimir como combinação linear das matrizes

de ordem

,
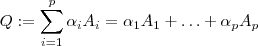
.
O elemento
![[Q]_{ij} [Q]_{ij}](/latexrender/pictures/9d2c530ca997c8489bd210ef64dd3032.png)
(situado no encontro da i-ésima linha com a j-ésima coluna de

) é escrito como
![\alpha_1 [A_1]_{ij} + \alpha_2 [A_2]_{ij} + \hdots + \alpha_p [A_p]_{ij} \alpha_1 [A_1]_{ij} + \alpha_2 [A_2]_{ij} + \hdots + \alpha_p [A_p]_{ij}](/latexrender/pictures/3bcee7b9f51c0ebda7f378982a65020c.png)
(
![[A_k]_{ij} [A_k]_{ij}](/latexrender/pictures/8934aeb9c7d6bcd8c91ad02f52520059.png)
termos gerais da matriz

) .
Assim , quando

, tem-se
![[Q]_{ij} = [A]_{ij} + [B]_{ij} - [C]_{ij} [Q]_{ij} = [A]_{ij} + [B]_{ij} - [C]_{ij}](/latexrender/pictures/05abe307a9745032bfeff564a24c2af1.png)
. Substituindo-se
![[A]_{ij} , [B]_{ij} [A]_{ij} , [B]_{ij}](/latexrender/pictures/77fe3a4e02bc87aa4c9a0cc6da4d2d5d.png)
e
![[C]_{ij} [C]_{ij}](/latexrender/pictures/4fa0bba10776a5511ee65b8ebe348739.png)
respectivamente pelas expressões correspondentes dadas terá uma expressão geral que determinar
![[Q]_{ij} [Q]_{ij}](/latexrender/pictures/9d2c530ca997c8489bd210ef64dd3032.png)
, fazendo
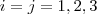
é possível determinar o que se pede no enunciado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ITA-SP) Elementos da diagonal principal do inverso
por Carolziiinhaaah » Qua Jun 23, 2010 18:15
- 2 Respostas
- 7967 Exibições
- Última mensagem por Carolziiinhaaah

Qua Jun 23, 2010 19:42
Matrizes e Determinantes
-
- Se A é uma matriz 5x5 cujos elementos fora da diagonal são n
por jlr2906 » Sáb Set 01, 2018 05:01
- 0 Respostas
- 4998 Exibições
- Última mensagem por jlr2906

Sáb Set 01, 2018 05:01
Álgebra Linear
-
- Qual o valor principal
por William Frank » Seg Nov 10, 2014 09:51
- 3 Respostas
- 2026 Exibições
- Última mensagem por William Frank

Qua Nov 12, 2014 22:59
Matemática Financeira
-
- Área e diagonal do paralelogramo/-help
por Trapezius » Qua Mai 31, 2017 01:38
- 0 Respostas
- 3146 Exibições
- Última mensagem por Trapezius

Qua Mai 31, 2017 01:38
Trigonometria
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7150 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 que se exprimir como combinação linear das matrizes
que se exprimir como combinação linear das matrizes  de ordem
de ordem  ,
, 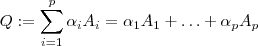 .
. ![[Q]_{ij} [Q]_{ij}](/latexrender/pictures/9d2c530ca997c8489bd210ef64dd3032.png) (situado no encontro da i-ésima linha com a j-ésima coluna de
(situado no encontro da i-ésima linha com a j-ésima coluna de  ) é escrito como
) é escrito como ![\alpha_1 [A_1]_{ij} + \alpha_2 [A_2]_{ij} + \hdots + \alpha_p [A_p]_{ij} \alpha_1 [A_1]_{ij} + \alpha_2 [A_2]_{ij} + \hdots + \alpha_p [A_p]_{ij}](/latexrender/pictures/3bcee7b9f51c0ebda7f378982a65020c.png) (
(![[A_k]_{ij} [A_k]_{ij}](/latexrender/pictures/8934aeb9c7d6bcd8c91ad02f52520059.png) termos gerais da matriz
termos gerais da matriz  ) .
) .  , tem-se
, tem-se ![[Q]_{ij} = [A]_{ij} + [B]_{ij} - [C]_{ij} [Q]_{ij} = [A]_{ij} + [B]_{ij} - [C]_{ij}](/latexrender/pictures/05abe307a9745032bfeff564a24c2af1.png) . Substituindo-se
. Substituindo-se ![[A]_{ij} , [B]_{ij} [A]_{ij} , [B]_{ij}](/latexrender/pictures/77fe3a4e02bc87aa4c9a0cc6da4d2d5d.png) e
e ![[C]_{ij} [C]_{ij}](/latexrender/pictures/4fa0bba10776a5511ee65b8ebe348739.png) respectivamente pelas expressões correspondentes dadas terá uma expressão geral que determinar
respectivamente pelas expressões correspondentes dadas terá uma expressão geral que determinar 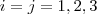 é possível determinar o que se pede no enunciado .
é possível determinar o que se pede no enunciado .
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
