Eu fiz assim:
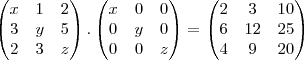
a11= 2x+0+0=2x=2 x=2
a22= 0+2y+0=2y=12 y=6
a33= 0+0+2z=20 z=10
A resposta certa é a B( 1,4,4)

(MACK) Sabe-se que
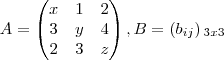 , é uma matriz diagonal, ou seja,
, é uma matriz diagonal, ou seja,  se i diferente j e
se i diferente j e 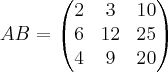 . Os valores de x, y e z são respectivamente:
. Os valores de x, y e z são respectivamente:a) 2,3, 4
b)1, 4, 4
c) 7,7,7
d) 2,3,1
e)1,1,1



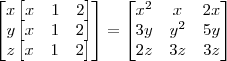
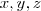 tal que os elementos da matriz à esquerda da igualdade sejam igual ao mesmo a direita da igualdade .
tal que os elementos da matriz à esquerda da igualdade sejam igual ao mesmo a direita da igualdade .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)