"Se
 é uma matriz
é uma matriz  x
x  tal que
tal que 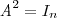 , então
, então 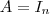 ou
ou 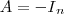 "
"Bom, como uma matriz multiplicada pela sua inversa sempre dá a matriz identidade, imaginei que a afirmação seja falsa, uma vez que para que
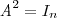 ,
,  .
.Não sei, entretanto, como colocar isso na resposta caso apareça em uma prova (ou qualquer questão similar) e se teria que exemplificar com um caso numérico para prova. É meu primeiro semestre na universidade, então não tenho muita noção de como funciona isso. Se alguém puder ajudar com essa ideia, agradeço muito!


 natural .Negar a afirmação entre aspas é o suficiente mostrar um contra exemplo . Vamos escolher n = 2 para simplificar e mostra que existe outra matriz
natural .Negar a afirmação entre aspas é o suficiente mostrar um contra exemplo . Vamos escolher n = 2 para simplificar e mostra que existe outra matriz  inversível diferente de
inversível diferente de  tal que
tal que  .Comece escrevendo
.Comece escrevendo 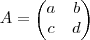 (vamos determinar a,b,c,d ) . Segue-se
(vamos determinar a,b,c,d ) . Segue-se  .
.  e
e  .
.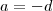 e
e  quaisquer .
quaisquer . 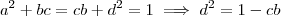 . Como
. Como 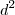 é sempre positivo , o lado direito também o é , escolhendo-se então
é sempre positivo , o lado direito também o é , escolhendo-se então 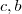 reais tais que
reais tais que 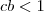 a solução geral do sistema será
a solução geral do sistema será  com
com 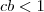 .
. e
e 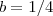 .Temos
.Temos 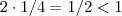 e
e 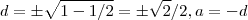
 tal que
tal que 

 .
.



