cramos_err escreveu:Mais a minha dúvida é pq 1/3, tem como vc fazer esse execício, para eu ver como fica, é apenas um exemplo.
Ao invés de "lhe dar o peixe", eu vou lhe "ensinar a pescar". Eu mostrarei o caminho e você tenta seguir. Se você não conseguir terminar, então poste aqui até onde conseguiu avançar.
Note que esse 1/3 é apenas um escalar multiplicando toda a matriz. Lembre-se que multiplicar um escalar por uma matriz é apenas realizar a seguinte operação:
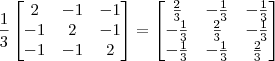
Agora bastaria calcular o produto:

Se o resultado desse produto for igual a matriz inicial, então a matriz é idempotente.
Mas ao invés de fazer por esse caminho, o mais interessante seria efetuar a seguinte arrumação:
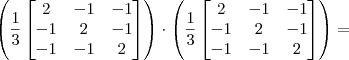
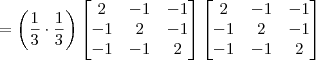
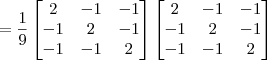
Agora basta calcular o produto entre as matrizes e comparar com a inicial. Note que esse produto é bem mais simples do que aquele entre as matrizes anteriores.
Tente continuar a partir daí.


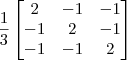

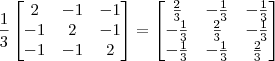

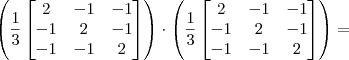
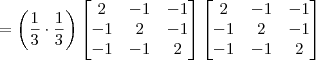
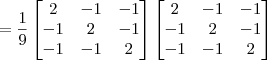
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
