 por Renan » Qui Jun 23, 2011 16:42
por Renan » Qui Jun 23, 2011 16:42
(UESPI) Se o determinante da matriz

é igual a 10, então o determinante da matriz
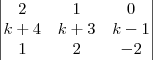
é igual a:
(a) 7
(b) 8
(c) 9(d) 10
(e) 11
Obs: Só entendi a quando determinantes trocam filas ou são multiplicados por um valor, mas não sei quando somados ou subtraídos.
-
Renan
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 23, 2011 16:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico em farmácia
- Andamento: formado
 por Molina » Qui Jun 23, 2011 16:47
por Molina » Qui Jun 23, 2011 16:47
Boa tarde, Renan.
Faça o primeiro determinante, que você tem o valor. Assim você descobrirá o valor de
k. Feito isso, substitua o valor de k no segundo determinante e calcule então o que você quer descobrir.
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Renan » Qui Jun 23, 2011 16:54
por Renan » Qui Jun 23, 2011 16:54
ahh sim, achei que envolvesse alguma propriedade referente a determinantes, já que duas linhas são iguais.
-
Renan
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 23, 2011 16:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico em farmácia
- Andamento: formado
 por FilipeCaceres » Qui Jun 23, 2011 17:11
por FilipeCaceres » Qui Jun 23, 2011 17:11
Uma outra forma seria,
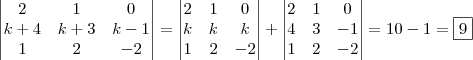
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Renan » Qui Jun 23, 2011 19:10
por Renan » Qui Jun 23, 2011 19:10
Sim, deve ser esse o objetivo da questão, já que está na lista das propriedades de determinantes. Obrigado, agora entendi.
-
Renan
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 23, 2011 16:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico em farmácia
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinante
por Jessi » Seg Abr 20, 2009 16:10
- 1 Respostas
- 3186 Exibições
- Última mensagem por Molina

Seg Abr 20, 2009 17:04
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Sex Set 10, 2010 22:00
- 5 Respostas
- 5393 Exibições
- Última mensagem por MarceloFantini

Dom Set 12, 2010 17:18
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Sáb Set 11, 2010 18:47
- 4 Respostas
- 4680 Exibições
- Última mensagem por DanielRJ

Dom Set 12, 2010 12:56
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Dom Set 12, 2010 15:54
- 3 Respostas
- 3971 Exibições
- Última mensagem por MarceloFantini

Seg Set 13, 2010 00:03
Matrizes e Determinantes
-
- (ITA) DETERMINANTE
por natanskt » Sáb Nov 20, 2010 10:26
- 4 Respostas
- 4299 Exibições
- Última mensagem por vitall

Ter Jan 04, 2011 02:42
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é igual a 10, então o determinante da matriz
é igual a 10, então o determinante da matriz 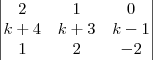

 é igual a 10, então o determinante da matriz
é igual a 10, então o determinante da matriz 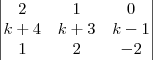




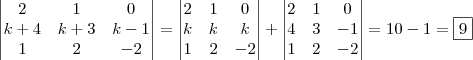


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.