 por Lucas Gabriel » Qua Fev 23, 2011 09:44
por Lucas Gabriel » Qua Fev 23, 2011 09:44
Sendo A = [-5 0 /-1 4] e B = [1-3/2 1] , resolva a equação 3X – A = 2B ( Obs: em A -5 é coluna com -1 e 0 com 4. Em b 1 coluna com 2 e -3 com 1). Não sei como resolver este tipo de equação. Quem souber e puder me ajudar muito obrigado.
-
Lucas Gabriel
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Fev 23, 2011 09:34
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Mecânica Industrial
- Andamento: cursando
 por Elcioschin » Qua Fev 23, 2011 11:20
por Elcioschin » Qua Fev 23, 2011 11:20
Não deu para entender
Se você não sabe usar o LaTeX, escreva assim:
A =
a ...... b
c ...... d
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por LuizAquino » Qua Fev 23, 2011 11:28
por LuizAquino » Qua Fev 23, 2011 11:28
Lucas Gabriel escreveu:Sendo A =
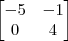
e B =
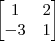
, resolva a equação 3X – A = 2B.
Você vai operar com a equação matricial 3X – A = 2B como se estivesse operando com uma equação convencional. Você só deve tomar cuidado com o produto entre matrizes (que de modo geral não é comutativo).
3X - A = 2B
3X = 2B + A


 Observação
ObservaçãoVale lembrar que se a equação fosse algo como AX=B, então você iria precisar calcular a inversa de A, isto é,
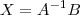
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por EduardoFavarin » Qua Mar 02, 2011 22:14
por EduardoFavarin » Qua Mar 02, 2011 22:14
A questão é a seguinte:

Sei que a resolução dela é por matrizes/regra de cramer... mas só que eu nao estou conseguindo aplicar. Me ajudem! grato...
-
EduardoFavarin
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mar 02, 2011 21:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qua Mar 02, 2011 22:55
por Elcioschin » Qua Mar 02, 2011 22:55
Eduardo
Por favor não utilize o tópico existente de alguma questão para postar uma nova questão.
Abra um novo tópico para colocar sua questão.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações de matrizes
por Li Rodrigues » Qui Jul 28, 2011 22:23
- 1 Respostas
- 1292 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:43
Matrizes e Determinantes
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5154 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3598 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 5998 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3153 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




e B =
, resolva a equação 3X – A = 2B.



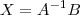 .
.




 .
.
 :
: