Bom dia!
Tentei fazer o problema abaixo de acordo com a fórmula An=A1.q^n-1, mas não consigo solucioná-lo. Coloquei a ordem para representar a idade dos irmãos: P.G. (x,y,z), depois tentei criar uma espécie de sistema do tipo: x.y.z=64, acrescentando que x+y=20, mas não consigo visualizar mais nada. Por favor, me ajudem. Segue o problema abaixo:
As idades de três irmãos são números inteiros que estão em P.G. Se o produto dessas idades é 64 e a soma das idades dos mais velhos é 20, quantos anos tem cada um dos irmãos?
Obrigada!


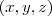
 (Razão da P.G)
(Razão da P.G)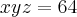 (Produto das raízes)
(Produto das raízes) (Soma das idades dos filhos mais velhos)
(Soma das idades dos filhos mais velhos)





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)