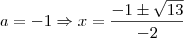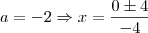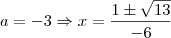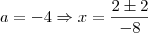Meu professor mandou um exercico muito complexo e ñ consigo resolver por favor alguem me ajuda
Os coeficientes a, b, c da equação de 2º grau ax^2 + bx + c = 0 são nessa ordem, termos de uma P.A. de razão 2.
A) Mostre que essa equação admite raizes reais para exatamente 4 valores inteiros de b, determinando-os.
B) Para cada valor encontrado no item anterior, determine raizes da equação.



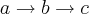 uma P.A. de razão 2, podemos fazer o seguinte -->
uma P.A. de razão 2, podemos fazer o seguinte --> 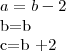
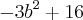 . Lembrando que valores menores que zero para discriminante não há raízes reais, logo
. Lembrando que valores menores que zero para discriminante não há raízes reais, logo 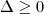 . Quando desenvolveres a desigualdade perceberás que os valores de b serão -
. Quando desenvolveres a desigualdade perceberás que os valores de b serão -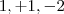 e
e 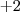 . Substitua esses valores lá na primeira equação e encontrarás 4 equações diferentes. veja quais delas são realmente de segundo grau e depois determine as raízes.. Fiz assim e consegui, mas pode haver um método mais simples ou posso ter errado em algum cálculo e ter me precipitado, bom, espero que consiga!
. Substitua esses valores lá na primeira equação e encontrarás 4 equações diferentes. veja quais delas são realmente de segundo grau e depois determine as raízes.. Fiz assim e consegui, mas pode haver um método mais simples ou posso ter errado em algum cálculo e ter me precipitado, bom, espero que consiga!
 não seria uma escolha interessante? Atende ao discriminante e continua sendo uma equação de segundo grau. Talvez quem montou o exercício imaginou a P.A. na forma
não seria uma escolha interessante? Atende ao discriminante e continua sendo uma equação de segundo grau. Talvez quem montou o exercício imaginou a P.A. na forma  ,
, 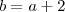 e
e 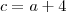 .
.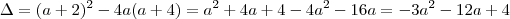
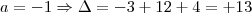
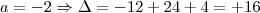
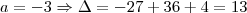
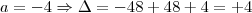
 pois senão não há equação do segundo grau. Com
pois senão não há equação do segundo grau. Com  , o discriminante é menor que zero e portanto não tem raízes reais. Com
, o discriminante é menor que zero e portanto não tem raízes reais. Com 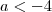 , discriminante volta a ser negativo, logo, existem somente 4 valores inteiros tais que a equação tenha solução.
, discriminante volta a ser negativo, logo, existem somente 4 valores inteiros tais que a equação tenha solução.