 por Emilia » Ter Fev 01, 2011 23:30
por Emilia » Ter Fev 01, 2011 23:30
1) Um dos maiores problemas das florestas brasileiras é o DESMATAMENTO. Suponhamos que em um dado momento uma floresta tenha ¼ de toda área desmatada, e que esse desmatamento cresça a uma taxa de 20% ao ano. Então:
a) Faça uma estimativa da área desmatada daqui a 4 anos, supondo que nesse período a área da floresta permaneça constante;
b ) Qual é a área desmatada em 4 anos sabendo que a área da floresta cresça a uma taxa de 10% ao ano? Seria possível fazer uma estimativa sobre a extinção total da floresta? Comente a sua resposta.
2) José decidiu nadar, regularmente, de quatro em quatro dias. Começou a fazê-lo em um sábado; nadou pela segunda vez na quarta-feira seguinte e assim por diante. Nesse caso, na centésima vez em que José for nadar, qual será o dia da semana?
3) A soma de três números que formam uma PA crescente é 36. Determine esses números, sabendo que, se somarmos 6 unidades ao último termo, eles passam a constituir uma PG.
Emilia
Novo Usuário
Mensagens: 5
Data de registro: Ter Nov 30, 2010 15:19
Formação Escolar: GRADUAÇÃO
Área/Curso: licenciatura em matemática
Andamento: cursando
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Qua Fev 02, 2011 12:57
por DanielFerreira » Qua Fev 02, 2011 12:57
3) A soma de três números que formam uma PA crescente é 36. Determine esses números, sabendo que, se somarmos 6 unidades ao último termo, eles passam a constituir uma PG.
P.Aa1 = x
a2 = y
a3 = z
Sn = 36
y - x = z - y
2y = x + z =========> x + z = 24
(I)temos que...
x + y + z = 36
y + 2y = 36
3y = 36
y = 12P.Ga1 = x
a2 = 12
a3 = z + 6
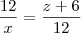
De
(I)...


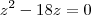

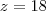
Daí,
x + y = 24
x + 18 = 24
x = 6Os números são 6, 12 e 18.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


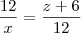


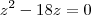

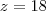

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.