 por damiana » Qua Out 27, 2010 20:55
por damiana » Qua Out 27, 2010 20:55
boa noite,tenho uma questão pra resolver e não consigo desenvolver apartir de determinado ponto. a questão pede assim: sendo 111um n° dividido em 3 partes,formam uma p.g de razão 3/4.qual será a menor parte.
comecei chamando essas 3 partes de a1, a2 e a3.ele me diz que foi dividido em 3 partes mas não me informa se foram iguais.não sei como desenvolver tive um ensino médio horrivel então não tenho muita base.
p.g: a1.q(n-1) 111/3= 37
a1= 37
a2=37x3/4(2-1)
....
me ajudem por favor
-
damiana
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Out 27, 2010 20:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Qua Out 27, 2010 21:23
por MarceloFantini » Qua Out 27, 2010 21:23
Vamos chamar as partes de
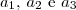
. A soma delas dá o número 111:

. Porém, sabemos também que eles formam uma P.G. de razão

:
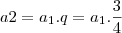
e
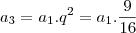
. Agora vamos juntar tudo:
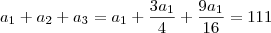
Multiplicando tudo por 16:
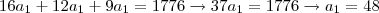
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


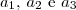 . A soma delas dá o número 111:
. A soma delas dá o número 111:  . Porém, sabemos também que eles formam uma P.G. de razão
. Porém, sabemos também que eles formam uma P.G. de razão  :
: 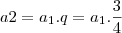 e
e 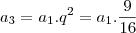 . Agora vamos juntar tudo:
. Agora vamos juntar tudo: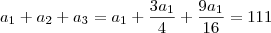
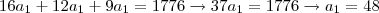


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.