-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 495114 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 554140 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 518111 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 749452 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2456171 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por antonybel » Seg Jul 18, 2022 22:41
por antonybel » Seg Jul 18, 2022 22:41
Em uma autoestrada há cinco saídas. As distâncias entre duas saídas consecutivas são todas iguais e a distância entre a segunda e a quarta saída é 36 km. A distância entre a primeira e a quinta saída, em quilômetros, é:
-
antonybel
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sex Nov 11, 2011 10:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Set 03, 2022 14:08
por DanielFerreira » Sáb Set 03, 2022 14:08
Olá
antonybel!
antonybel escreveu:Em uma autoestrada há cinco saídas. As distâncias entre duas saídas consecutivas são todas iguais e a distância entre a segunda e a quarta saída é 36 km. A distância entre a primeira e a quinta saída, em quilômetros, é:
Sejam
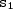
,
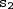
,
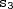
,
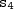
e

as saídas da autoestrada. De acordo com o enunciado,

. Posto isto, determinemos

. Segue:

Logo,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 8724 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
-
- Questão de concurso
por bia rosendo » Qua Fev 23, 2011 11:00
- 4 Respostas
- 5196 Exibições
- Última mensagem por Elcioschin

Qui Fev 24, 2011 11:08
Funções
-
- Questão de concurso
 por bia rosendo » Seg Fev 28, 2011 22:54
por bia rosendo » Seg Fev 28, 2011 22:54
- 2 Respostas
- 7299 Exibições
- Última mensagem por LuizAquino

Ter Mar 01, 2011 14:12
Problemas do Cotidiano
-
- QUESTAO CONCURSO..
por PathyNorato » Qui Jul 07, 2011 15:59
- 1 Respostas
- 3051 Exibições
- Última mensagem por FilipeCaceres

Qui Jul 07, 2011 21:05
Matemática Financeira
-
- questão de concurso
por luciana-lopfer » Qui Nov 24, 2011 14:34
- 5 Respostas
- 5662 Exibições
- Última mensagem por Tiago_Cariolano

Seg Jan 16, 2012 01:23
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



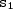 ,
, 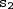 ,
, 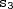 ,
, 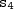 e
e  as saídas da autoestrada. De acordo com o enunciado,
as saídas da autoestrada. De acordo com o enunciado,  . Posto isto, determinemos
. Posto isto, determinemos  . Segue:
. Segue:



 .
.
 :
: