Professor, estou a dias tentando resolver esse problema, montei ate um esquema desenhado e sempre chego na resposta de 1311 sendo assim não consigo chegar na resposta do gabarito. por gentileza me ajuda. Segue a questão
10 m 1,5 m 1,5 m 1,5 m 1,5 m
1ª 2ª 3ª 4ª 50ª 51ª Torneira
3
Em um caminho retilíneo há um canteiro formado por
51 roseiras, todas enfileiradas ao longo do caminho, como
ilustrado. A distância entre quaisquer duas roseiras conse-
cutivas é 1,5 m. Nesse caminho, há ainda uma torneira a
10,0 m da primeira roseira.
Gabriel decide molhar todas as roseiras desse caminho. Para
isso, utiliza um regador que, quando cheio, tem capacidade
para molhar 3 roseiras.
Dessa forma, Gabriel enche o regador na torneira, encaminha-se
para a 1a
roseira, molha-a, caminha até a 2a
roseira,
molha-a e, a seguir, caminha até a 3a
roseira, molhando-a
também, esvaziando o regador. Cada vez que o regador fica
vazio, Gabriel volta à torneira, enche o regador e repete a
rotina anterior para as três roseiras seguintes. No momento
em que acabar de regar a última das roseiras, quantos metros
Gabriel terá percorrido ao todo desde que encheu o regador
pela primeira vez?
(A) 1666,0 (B) 1581,0
(C) 1496,0 (D) 833,0
(E) 748,0


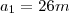 ;
;  ;
; 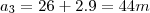 (...)
(...) 
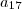 .
. 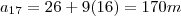
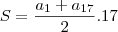

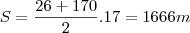

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)