Pense que a

-ésima linha será formada por
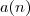
alunos. É fácil de perceber que a quantidade de alunos da p´roxima linha, isto é, da linha de número

será tal que
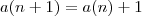
Ou seja, a quantidade de alunos da próxima linha será Sempre a quantidade de alunos da linha anterior mais um aluno.
Reconhece esse comportamento? É uma P.A.! Já que a razão é 1 e a quantidade de alunos na primeira fila é 1, então o termo geral será
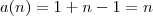
Agora, aplique a fórmula de soma de uma P.A. e calcule para qual

que a mesma vale 210.
Tão simples quanto isso.



 -ésima linha será formada por
-ésima linha será formada por 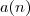 alunos. É fácil de perceber que a quantidade de alunos da p´roxima linha, isto é, da linha de número
alunos. É fácil de perceber que a quantidade de alunos da p´roxima linha, isto é, da linha de número  será tal que
será tal que 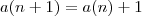
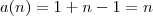
 que a mesma vale 210.
que a mesma vale 210.


 .
.
 :
: