 por netolucen4 » Qua Jun 26, 2013 20:47
por netolucen4 » Qua Jun 26, 2013 20:47
Pessoal como proceder para resolver

os dados seriam esses?
![{a}_{1} = \sqrt[3]{\pi} {a}_{1} = \sqrt[3]{\pi}](/latexrender/pictures/f27b1ab6f279472b57d6e61677141a18.png)
q =
![\frac{1}{\sqrt[9]{{\pi}^{2}}} \frac{1}{\sqrt[9]{{\pi}^{2}}}](/latexrender/pictures/f974773a12aa09d938e745e2ec6fbcaa.png)
mas não temos nem a quantidade de termos nem o último termo...
para resolver teríamos que usar o
![{P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}} {P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}}](/latexrender/pictures/61ed6eeaba018160d6360226baaa302d.png)
?
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Jun 27, 2013 23:02
por young_jedi » Qui Jun 27, 2013 23:02
primeiro vamos reescrever esse produto
![\sqrt[3]\pi\sqrt[9]\pi\sqrt[27]\pi\dots=\pi^{\frac{1}{3}}.\pi^{\frac{1}{9}}.\pi^{\frac{1}{27}}\dots \sqrt[3]\pi\sqrt[9]\pi\sqrt[27]\pi\dots=\pi^{\frac{1}{3}}.\pi^{\frac{1}{9}}.\pi^{\frac{1}{27}}\dots](/latexrender/pictures/cefd9ecfb21db9f5f78330c17a01255a.png)
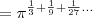
repare que o expoente de pi é a soma de uma progressão geométrica infinita de razão 1/3, é so utilizar a equação da soma para progressão geométrica de razão menor que 1 e você econtrara o resultado, comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netolucen4 » Sex Jun 28, 2013 03:08
por netolucen4 » Sex Jun 28, 2013 03:08
Young primeiramente muito obrigado, fico muito grato por suas respostas...
Seria assim...

e encontraríamos o
![{\pi}^{\frac{1}{2}} = \sqrt[]{\pi} {\pi}^{\frac{1}{2}} = \sqrt[]{\pi}](/latexrender/pictures/2cc3e251e6202ba209c1600adcb5f0f5.png)
e o G =
![\sqrt[]{\pi} \sqrt[]{\pi}](/latexrender/pictures/19b7d518ae55b0c142022e4f6e8bbda6.png)
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sex Jun 28, 2013 10:35
por young_jedi » Sex Jun 28, 2013 10:35
Exatamente, é isso mesmo!!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4243 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4721 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25517 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4232 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2885 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![{a}_{1} = \sqrt[3]{\pi} {a}_{1} = \sqrt[3]{\pi}](/latexrender/pictures/f27b1ab6f279472b57d6e61677141a18.png)
![\frac{1}{\sqrt[9]{{\pi}^{2}}} \frac{1}{\sqrt[9]{{\pi}^{2}}}](/latexrender/pictures/f974773a12aa09d938e745e2ec6fbcaa.png)
![{P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}} {P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}}](/latexrender/pictures/61ed6eeaba018160d6360226baaa302d.png) ?
?

![{a}_{1} = \sqrt[3]{\pi} {a}_{1} = \sqrt[3]{\pi}](/latexrender/pictures/f27b1ab6f279472b57d6e61677141a18.png)
![\frac{1}{\sqrt[9]{{\pi}^{2}}} \frac{1}{\sqrt[9]{{\pi}^{2}}}](/latexrender/pictures/f974773a12aa09d938e745e2ec6fbcaa.png)
![{P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}} {P}_{n} = \sqrt[2]{{\left({a}_{1}.{a}_{n} \right)}^{n}}](/latexrender/pictures/61ed6eeaba018160d6360226baaa302d.png) ?
?
![\sqrt[3]\pi\sqrt[9]\pi\sqrt[27]\pi\dots=\pi^{\frac{1}{3}}.\pi^{\frac{1}{9}}.\pi^{\frac{1}{27}}\dots \sqrt[3]\pi\sqrt[9]\pi\sqrt[27]\pi\dots=\pi^{\frac{1}{3}}.\pi^{\frac{1}{9}}.\pi^{\frac{1}{27}}\dots](/latexrender/pictures/cefd9ecfb21db9f5f78330c17a01255a.png)
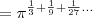


![{\pi}^{\frac{1}{2}} = \sqrt[]{\pi} {\pi}^{\frac{1}{2}} = \sqrt[]{\pi}](/latexrender/pictures/2cc3e251e6202ba209c1600adcb5f0f5.png)
![\sqrt[]{\pi} \sqrt[]{\pi}](/latexrender/pictures/19b7d518ae55b0c142022e4f6e8bbda6.png)



 .
.
 :
: