por Erico gremio » Dom Abr 14, 2013 14:41
Dada uma fita separada em intervalos horizontais por
três cores: azul, amarelo e branco, onde há repetição dessas cores.
Se a primeira cor que vemos é amarelo, a segunda azul e a terceira
branca, qual será a cor do intervalo de número 1000000?
-
Erico gremio
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Qui Abr 11, 2013 18:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
por nakagumahissao » Dom Abr 14, 2013 14:47
Poderia nos dizer o que já tentou fazer para resolver este problema por favor? Veja as regras deste fórum em caso de dúvidas.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário
-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
por Erico gremio » Dom Abr 14, 2013 15:31
o meu raciocínio foi o seguinte: como
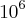o expoente é 6 e o 6 é par e é divisível por 3. Como a ultima cor a branca, logo
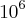é a cor branco.
Mais não sei se esta certo!
-
Erico gremio
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Qui Abr 11, 2013 18:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
por nakagumahissao » Dom Abr 14, 2013 18:15
Veja bem Erico Gremio,
A cor azul aparece da seguinte maneira: 1, 4, 7, 10,...
A cor amarela aparece da seg. maneira: 2, 5, 8, 11,...
A cor branca aparece da seguinte maneira: 3, 6, 9, 12,...
Note que seu raciocínio está quase correto, mas observe que quando azul é 1, amarelo é 2 e branco é 3, em seguida, quando azul é 4, amarelo é 5 e branco é 6 e assim por diante, ou seja, sempre 1 acima do anterior. Logo:
Pegando-se apenas a parte inteira, tem-se 333.333 que multiplicado por 3 dará 999999. Este é o último branco. O Próximo será então Azul na posição 1000000.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário
-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
