Progressão aritmética

[Lucio]

Olas colegas...
Se enumeram de 1 até n as páginas de um livro. Ao somar esses números, por engano, um deles é somado
duas vezes, obtendo-se o resultado incorreto: 1986. O valor de n e o número da página que foi
somado duas vezes são?

1º - Tentei por soma de PA, não consegui;
2º - Tentei pela fórmula = 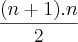pois é um número triangular,

percebi que estava trabalhando com a soma de PA e não cheguei ao resultado.
Será que tem um outro caminho para a resolução?

Desde já agradeço a atenção de todos
Abraços

[Cleyson007]

A sequência das páginas do livro formam uma P.A de n termos e 1°termo igual a 1. Logo:

S = (n² + n)/2

Considerando que não houvesse a inclusão do número repetido, teríamos:

(n² + n)/2 = 1686
n² + n = 2 (1686) = 3372
n² + n - 3372 = 0

Por Bháskara, temos:
? = 1² - 4*(-3372) = 1 + 13488 = 13489
?? = ?13489 = ±116,14...

Pelo fato de ter tido acréscimo do número repetido, vemos que ?? deverá ser 116 ou 115. Logo:
n = (-1 + 116)/2 ou (-1 + 115)/2

Cujos resultados seriam
n = 115/2 ou 114/2.

Ora, o primeiro deles não serve, pois resultaria em um "n" fracionário; logo,
n = 114/2
n = 57

Quanto ao número da página que foi somado duas vezes:
S = (1 + 57)*57/2 = 58*57/2 = 58/2 * 57 = 29*57 = 1653

1686 - 1653 = 33

Solução:

n = 57

nº da página = 33

[young_jedi]

eu encontrei como resposta n=62



temos que

portanto o livro pode ter 62 paginas e ter somando por engano duas vezes a pagina 33

Na resposta do Cleyson ele utilizou 1686 mais o correto é 1986 mais o procedimento para se chegar na resposta é esse mesmo

[Lucio]

Cleyson007 e Young_jedi.

Muito obrigado pelo apoio.

Abraços.