 por 404040 » Seg Out 18, 2010 18:27
por 404040 » Seg Out 18, 2010 18:27
Se nº 111 for dividido em três partes, que constituem uma PG de razão 3/4, a menor desssas partes será :
Estou quebrando a cabeça mas não consigo nem começar o cálculo...
-
404040
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 17, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por VtinxD » Sáb Out 23, 2010 03:18
por VtinxD » Sáb Out 23, 2010 03:18
Podemos escrever uma PG desta forma:
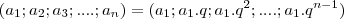
.Sendo

o termo independente ,

o n-ésimo termo e "q" a razão da PG.
Como o numero 111 foi dividido em três partes em PG logo podem ser escritos da for utilizada acima ,como são apenas 3 números em PG podemos utilizar os tres primeiros termos da dela.

.Como
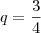
temos:

.Tirando o mmc:

Como a PG é decrecente, graças a sua razão menor do que 1,o menor termo não é

e sim
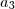
.
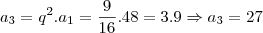
Espero ter ajudado e me desculpe qualquer erro mas são 3 da manhã

.Boa noite
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por 404040 » Sáb Out 23, 2010 09:21
por 404040 » Sáb Out 23, 2010 09:21
Agradeço muito a boa vontade, principalmente neste horário, sua explicação foi ótima, simples e prática, valeu...
-
404040
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 17, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



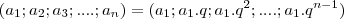 .Sendo
.Sendo  o termo independente ,
o termo independente ,  o n-ésimo termo e "q" a razão da PG.
o n-ésimo termo e "q" a razão da PG. .Como
.Como 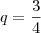 temos:
temos: .Tirando o mmc:
.Tirando o mmc:
 e sim
e sim 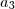 .
.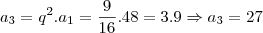
 .Boa noite
.Boa noite


 , avisa que eu resolvo.
, avisa que eu resolvo.

