bem eu comecei a fazer assim:
se:
a4 * a7 = 512 então a5 * a6 = 512
aí eu peguei e fiz assim:
a5 * (a5 * q) = 512
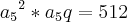
mas não consegui sair daí, o que fiz de errado?

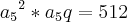




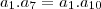

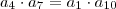 porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com
porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com  .
.

Fantini escreveu:Sim,porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com
.
 e
e 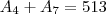 poderia fazer isso tambem?
poderia fazer isso tambem?







Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante