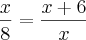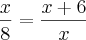por Nosbor » Qui Ago 26, 2010 01:13
por Nosbor » Qui Ago 26, 2010 01:13
Olá. Não estou conseguindo resolver essas PGs. Alguém me ajuda?
8,x,x+6
Estou tentando resolver da seguinte forma:
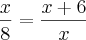
x²=8x+48
-x²+8x+48=0
Chegando aí, eu utilizo Bhaskara. Só que não dá o resultado certo.
Obrigado.
-
Nosbor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jul 08, 2010 20:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Nosbor » Qui Ago 26, 2010 02:04
por Nosbor » Qui Ago 26, 2010 02:04
Não acredito!
Caramba! Revisando minhas contas achei o erro. Tinha esquecido de fazer a raiz de 256.
Obrigado.
Até mais.
-
Nosbor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jul 08, 2010 20:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.